
【题目】如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移到△DCE,连接AD,BD,下列结论错误的是( )
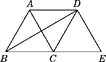
A.AD=BCB.BD⊥DE
C.四边形ACED是菱形D.四边形ABCD的面积为4![]()
【答案】D
【解析】
由△ABC沿射线BC向右平移到△DCE,根据平移的性质:对应点的连线平行且相等得到AD与BC平行且相等,选项A正确,利用一组对边平行且相等的四边形为平行四边形得到ABCD为平行四边形,由三角形ABC为等边三角形可得出AB=BC,根据邻边相等的平行四边形为菱形可得出四边形ABCD为菱形,根据菱形的对角线互相垂直得到AC与BD垂直,再由平移的性质得到对应边平行,得到AC与DE平行,利用与平行线中的一条垂直,与另一条也垂直得到BD垂直于DE,选项B正确;同理可得出ACED为菱形,选项C正确;过A作AF垂直于BC,由三角形ABC为边长为2的等边三角形,根据三线合一得到BF为BC的一半,求出BF的长,在直角三角形ABF中,由AB及BF的长,利用勾股定理求出AF的长,然后利用底BC乘以高AF即可求出菱形ABCD的面积为2![]() ,选项D错误,即可得出满足题意的选项.
,选项D错误,即可得出满足题意的选项.
∵△ABC沿射线BC向右平移到△DCE,
∴AD=BC,AD∥BC,故选项A正确;
∴四边形ABCD为平行四边形,
又△ABC为等边三角形,∴AB=BC,
∴四边形ABCD为菱形,
∴AC⊥BD,
由平移可知:AC∥DE,
则DE⊥BD,故选项B正确;
∵△ABC沿射线BC向右平移到△DCE,
∴AD=CE,AD∥CE,
∴四边形ACED为平行四边形,
由平移可得△DCE也为等边三角形,
∴DE=CE,
∴四边形ACED为菱形,选项C正确;
过A作AF⊥BC,如图所示:
∵△ABC为边长为2的等边三角形,
∴BF=CF=![]() BC=1,
BC=1,
在Rt△ABF中,AB=2,BF=1,
根据勾股定理得:AF=![]() ,
,
则S菱形ABCD=BCAF=2![]() ,选项D错误,
,选项D错误,
则原题结论错误的选项为D.
故选:D.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
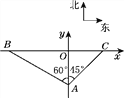
【题目】在某段限速公路BC上(公路视为直线),交通管理部门规定汽车的最高行驶速度不能超过60 km/h(即![]() ),并在离该公路100 m处设置了一个监测点A.在如图的平面直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.另外一条公路在y轴上,AO为其中的一段.
),并在离该公路100 m处设置了一个监测点A.在如图的平面直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.另外一条公路在y轴上,AO为其中的一段.
(1)求点B和点C的坐标;
(2)一辆汽车从点B匀速行驶到点C所用的时间是15 s,通过计算,判断该汽车在这段限速路上是否超速.(参考数据: ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽学完统计知识后,随机调查了她所在辖区若干名居民的年龄,并绘制成如下统计图.
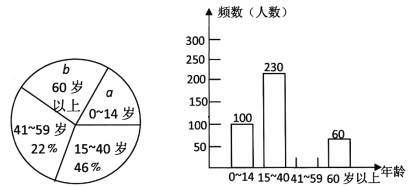
请根据统计图提供的信息,解答下列问题
(1)小丽共调查了 名居民的年龄,扇形统计图中a= %,b= %;
(2)补全条形统计图;
(3)若该辖区0~14岁的居民约有3500人,请估计年龄在60岁以上的居民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
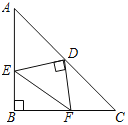
【题目】在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,则EF的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,两直角边AC=8cm,BC=6cm.
(1)作∠BAC的平分线AD交BC于点D;(尺规作图,不写作法,保留作图痕迹)
(2)计算△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=BC=4,点D在边BC上,以AD为折痕,将△ABD折叠,得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com