
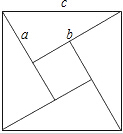
 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为12+6$\sqrt{3}$.
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为12+6$\sqrt{3}$. 分析 根据小正方形的面积为3,求出小正方形的边长为$\sqrt{3}$,即b-a=$\sqrt{3}$,然后根据直角三角形中较小的锐角为30°,可得b=$\sqrt{3}$a,联立两式求出a、b的值.继而可求出大正方形的面积.
解答 解:∵小正方形的面积为3,
∴小正方形的边长为$\sqrt{3}$,
即b-a=$\sqrt{3}$,
∵直角三角形中较小的锐角为30°,
∴b=$\sqrt{3}$a,
解得:a=$\frac{3+\sqrt{3}}{2}$,b=$\frac{3+3\sqrt{3}}{2}$,
∵大正方形的面积=c2=a2+b2,
∴大正方形的面积=($\frac{3+\sqrt{3}}{2}$)2+($\frac{3+3\sqrt{3}}{2}$)2=12+6$\sqrt{3}$.
故答案为:12+6$\sqrt{3}$.
点评 此题主要考查了勾股定理的应用,解答本题的关键是熟练掌握勾股定理以及三角函数的知识.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在港口A的南偏东49°方向有一座小岛B,在港口A的南偏西26°方向有一个小岛C,一艘轮船以每小时20海里的速度从港口A出发,向小岛B航行,经过5小时到达小岛B,这时测得小岛C在小岛B的南偏西71°方向,求小岛B距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
如图所示,在港口A的南偏东49°方向有一座小岛B,在港口A的南偏西26°方向有一个小岛C,一艘轮船以每小时20海里的速度从港口A出发,向小岛B航行,经过5小时到达小岛B,这时测得小岛C在小岛B的南偏西71°方向,求小岛B距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
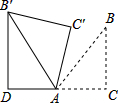 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com