
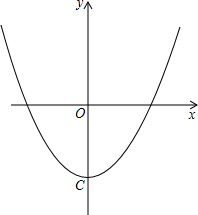
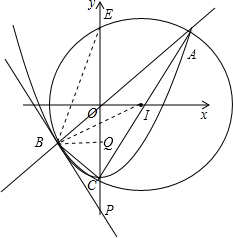
 已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.
已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.| 2 |
| 2 |
| 5 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 2 |
| 5 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
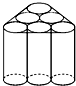 新学期开学,光明中学开展了一项名为“提倡节约,回收利用,从我做起”的活动.九年级(2)班李琼同学利用废旧的易拉罐制作了一个笔筒(罐与罐之间已用双面胶封紧),如图所示.为了美观,现欲将笔筒的侧面包上礼品纸,已知易拉罐的半径为r,高为h,则需礼品纸的面积为
新学期开学,光明中学开展了一项名为“提倡节约,回收利用,从我做起”的活动.九年级(2)班李琼同学利用废旧的易拉罐制作了一个笔筒(罐与罐之间已用双面胶封紧),如图所示.为了美观,现欲将笔筒的侧面包上礼品纸,已知易拉罐的半径为r,高为h,则需礼品纸的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
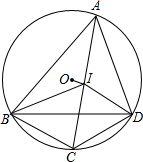 如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com