
 如图,直线l1:y1=k1x+b1经过点A(0,4),点D(4,0),直线l2:y2=k2x+b2与x轴交于点C,两直线l1、l2相交于点B,点B的纵坐标为2.
如图,直线l1:y1=k1x+b1经过点A(0,4),点D(4,0),直线l2:y2=k2x+b2与x轴交于点C,两直线l1、l2相交于点B,点B的纵坐标为2. 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
 文艺演出时,节目主持人站在舞台的黄金分割点处最能使人产生美感.如图,舞台AB长为30m,主持人站在离A点约11.5m的C处较恰当.当她从C点向B点再走
文艺演出时,节目主持人站在舞台的黄金分割点处最能使人产生美感.如图,舞台AB长为30m,主持人站在离A点约11.5m的C处较恰当.当她从C点向B点再走查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:
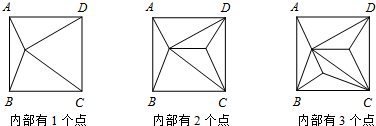
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数m | 4 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com