

分析 (1)根据BE∥AC得S△ACE=S△ACB,所以S△AED=S梯形ABCD,再根据中线性质即可解决.
(2)证明类似(1).
解答 解:(1)如图1中,∵AB∥EC,AB=EC,
∴四边形ABEC是平行四边形,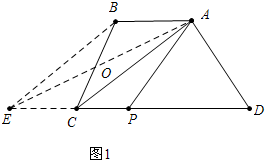
∴BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∴S△AED=S梯形ABCD,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=$\frac{1}{2}$S△AED=$\frac{1}{2}$S梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中,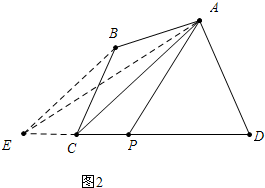 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=$\frac{1}{2}$S△AED=${\frac{1}{2}S}_{梯形ABCD}$.
点评 本题考查四边形的面积、三角形的中线的性质、以及同底等高的两个三角形面积等知识,把梯形面积转化为三角形面积是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 211 | B. | 212 | C. | 232 | D. | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\frac{{\sqrt{15}}}{5}$或$\frac{{\sqrt{15}}}{3}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,且y关于x的函数图象大致如图:
如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,且y关于x的函数图象大致如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过A作AT⊥BE于T点,写出AT+TE与BE之间的数量关系.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过A作AT⊥BE于T点,写出AT+TE与BE之间的数量关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com