Question

4．如图，在直角三角形ABC中，∠C=90°，AC=4，BC=3，一条与AB垂直的动直线从点A开始沿AB方向移动，移动到点B则停止，在移动的过程中，动直线与AB交于D，与AC或BC交于点E．
（1）如图①沿DE折叠，当点A与点B恰好重合时，请求出CE的长；
（2）请探究：在移动的过程中，是否存在动直线与△ABC的两边围成的三角形的面积为2？如果存在，请说明理由，并指出这样的三角形的个数；如果不存在，请说明理由．

Answer 1

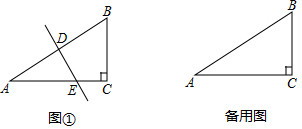
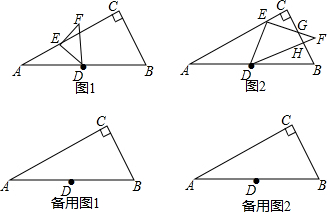
分析 （1）如图①，连结BE，设CE=x，在Rt△BCE中，根据勾股定理可得关于x的方程，解方程即可求出CE的长；
（2）根据三角形面积公式即可求解．

解答 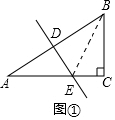解：（1）如图①，连结BE，
设CE=x，
在Rt△BCE中，依题意有（4-x）²=x²+3²，
解得x=$\frac{7}{8}$．
故CE的长是$\frac{7}{8}$；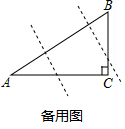
（2）如备用图，
设一条直角边为3x，则另一条直角边为4x，依题意有
3x×4x÷2=2，
解得x=±$\frac{\sqrt{3}}{3}$（负值舍去），
3x=$\sqrt{3}$，
4x=$\frac{4\sqrt{3}}{3}$．
故存在动直线与△ABC的两边围成的三角形的面积为2，这样的三角形的个数是2个．

点评 此题考查了翻折变换（折叠问题），勾股定理，三角形面积，解题时应分别对每一个图形进行仔细分析，难度不大．