
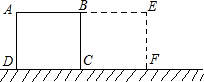
 已知正方形纸片ABCD的边长AB=2cm,把正方形ABCD绕某一点按顺时针方向旋转,使它旋转后能与正方形BEFC重合.
已知正方形纸片ABCD的边长AB=2cm,把正方形ABCD绕某一点按顺时针方向旋转,使它旋转后能与正方形BEFC重合.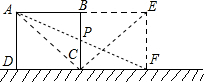 解:(1)∵正方形纸片ABCD和正方形BEFC形成了矩形,又正方形ABCD绕某一点按顺时针方向旋转,
解:(1)∵正方形纸片ABCD和正方形BEFC形成了矩形,又正方形ABCD绕某一点按顺时针方向旋转,| 2 |
| 5 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
(2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
| 1 |
| 3 |
 |
| AB |
| 19 |
| 3 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图可折成的正方体的体积为( )
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图可折成的正方体的体积为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.
如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.查看答案和解析>>
科目:初中数学 来源:2012-2013学年江西省景德镇市八年级下学期期末质量检测数学试卷(带解析) 题型:单选题
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点。已知BC=24cm,则这个展开图可折成的正方体的体积为( ) 
| A.64cm3 | B.27cm3 | C.9cm3 | D.8cm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com