
【题目】如图,已知抛物线y= ![]() x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式;
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE= ![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
【答案】
(1)解:∵抛物线 ![]() 与y轴交于点C ∴C(0,n)
与y轴交于点C ∴C(0,n)
∵BC∥x轴 ∴B点的纵坐标为n
∵B、A在y=x上,且OA=OB∴B(n,n),A(-n,-n)
∴ 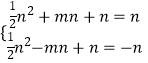 解得:n=0(舍去),n=-2;m=1
解得:n=0(舍去),n=-2;m=1
∴所求解析式为: ![]()
(2)解:作DH⊥EG于H
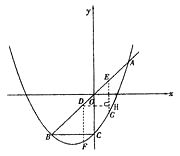
∵D、E在直线y=x上 ∴∠EDH=45![]() ∴DH=EH
∴DH=EH
∵DE= ![]() ∴DH=EH=1 ∵D(x,x) ∴E(x+1,x+1)
∴DH=EH=1 ∵D(x,x) ∴E(x+1,x+1)
∴F的纵坐标: ![]() ,G的纵坐标:
,G的纵坐标: ![]()
∴DF= ![]() -(
-( ![]() )=2-
)=2- ![]() EG=(x+1)- [
EG=(x+1)- [ ![]() ]=2-
]=2- ![]()
∴ ![]()
![]()
![]()
∴x的取值范围是-2<x<1 当x=- ![]() 时,y最大值=3
时,y最大值=3 ![]()
【解析】 (1)根据题意求出C点的坐标,根据平行于x轴的直线上的点纵坐标相同得出B点的纵坐标为n ,又因B、A在y=x上,故A,B两点的横坐标与纵坐标分别相同,且OA=OB,从而得出B(n,n),A(-n,-n),将A,B两点的坐标分别代入函数解析式得出方程组,解出m,n的值,从而得出解析式;
(2)作DH⊥EG于H,由∵D、E在直线y=x上 故∠EDH=45![]() 根据等腰直角三角形的性质得出DH=EH,根据勾股定理得出DH=EH=1,从而知D(x,x) E(x+1,x+1),进而根据抛物线上点的坐标特点表示出F的纵坐标,G的纵坐标,DF,EG的长度,根据梯形的面积公式列出y与x的函数关系式。
根据等腰直角三角形的性质得出DH=EH,根据勾股定理得出DH=EH=1,从而知D(x,x) E(x+1,x+1),进而根据抛物线上点的坐标特点表示出F的纵坐标,G的纵坐标,DF,EG的长度,根据梯形的面积公式列出y与x的函数关系式。


科目:初中数学 来源: 题型:
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,如图A、B两点之间的距离表示为AB,记作AB=|a﹣b|.回答下列问题:
(1)数轴上表示2和5两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
(2)已知|a﹣3|=7,则有理数a= ;
(3)若数轴上表示数b的点位于﹣4与3的两点之间,则|b﹣3|+|b+4|= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 ![]() ,那么AC= .
,那么AC= . 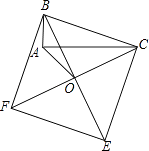
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
(1)当a=1时,则点Q的坐标为;
(2)当点P在直线上运动时,点Q也随之运动.当a=时,AQ+BQ的值最小为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si39°≈0.63,cos39°≈0.78,tan39°≈0.81.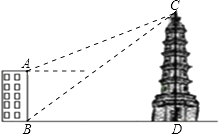
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com