
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,过
的中点,过![]() 点的直线分别交
点的直线分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() ,
,![]() 在对角线
在对角线![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() .
.
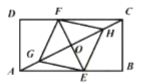
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)5
【解析】
(1)根据矩形性质得对边平行,再得内错角相等,证明△CFO≌△AEO,得EO=FO,进而根据对角线互相平分的四边形是平行四边形即证;(2)根据定义证明四边形EGFH是菱形,其性质为对角线互相垂直,通过证△AOE∽△ABC,得对应边成比例列式计算.
解:(1)∵四边形ABCD是矩形,
∴CD∥AB,
∴∠DCA=∠CAB,∠CFE=∠AEF,
∵O为AC的中点,
∴CO=AO,
∴△CFO≌△AEO,
∴EO=FO,
∵CO=AO,AG=CH,
∴OH=OG,
∵EO=FO,OH=OG,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)∵EG=EH,
∴平行四边形EGFH是菱形,
∴EF⊥AC,
∴∠AOE=90°
∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=4
∵AB=8,
∴由勾股定理得,AC=![]() ,
,
∴AO=![]() .
.
∵∠AOE=∠B=90°, ∠OAE=∠BAC,
∴△AOE∽△ABC,
∴![]() ,即
,即![]()
∴AE=5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
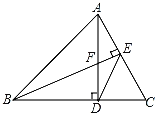
【题目】如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.
(1)求证:△AEF∽△BDF;
(2)若AE=4,BD=8,EF+DF=9,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
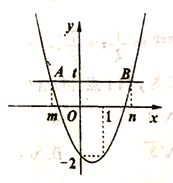
【题目】如图为二次函数![]() 图象,直线
图象,直线![]() 与抛物线交于
与抛物线交于![]() 两点,
两点,![]() 两点横坐标分别为
两点横坐标分别为![]() 根据函数图象信息有下列结论:
根据函数图象信息有下列结论:
①![]() ;
;
②若对于![]() 的任意值都有
的任意值都有![]() ,则
,则![]() ;
;
③![]() ;
;
④![]() ;
;
⑤当![]() 为定值时若
为定值时若![]() 变大,则线段
变大,则线段![]() 变长
变长
其中,正确的结论有__________(写出所有正确结论的番号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 。
。
(1)该二次函数图象的对称轴是_____________________;
(2)若该二次函数的图象开口向上,当![]() 时,函数图象的最高点为
时,函数图象的最高点为![]() ,最低点为
,最低点为![]() ,点
,点![]() 的纵坐标为11,求点
的纵坐标为11,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)对于该二次函数图象上的两点![]() ,设
,设![]() ,当
,当![]() 时,均有
时,均有![]() ,请结合图象,求出
,请结合图象,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据对徐州市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数![]() 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数![]() 的图象如图②所示.
的图象如图②所示.

(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时 获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com