
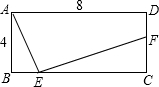
 已知如图,矩形ABCD中,E、F分别是边BC、CD上的点,AB=4,AD=8,CF=3,若△ABE与以E、C、F为顶点的三角形相似,则BE的长为________.
已知如图,矩形ABCD中,E、F分别是边BC、CD上的点,AB=4,AD=8,CF=3,若△ABE与以E、C、F为顶点的三角形相似,则BE的长为________.
 解:设BE=x,
解:设BE=x,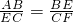 ,
, ,
, ,
, ,
, ,
, .
. .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
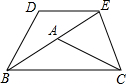 (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连结CE.

(1)则四边形DBCE是_______形(填写:平行四边形、矩形、菱形、正方形、梯形)
(2)若AB=AC=1,BC=![]() ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.
查看答案和解析>>
科目:初中数学 来源:2012届北京市通州区九年级中考一模数学卷(带解析) 题型:解答题
已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连结CE.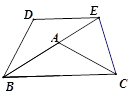
(1)则四边形DBCE是_______形(填写:平行四边形、矩形、菱形、正方形、梯形)
(2)若AB=AC=1,BC=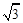 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市通州区九年级中考一模数学卷(解析版) 题型:解答题
已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连结CE.

(1)则四边形DBCE是_______形(填写:平行四边形、矩形、菱形、正方形、梯形)
(2)若AB=AC=1,BC=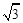 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE. ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com