
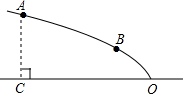
 ��ͼ��ij�㳡��Ƶ�һ���������͵��ݽ����������ߵ�һ���֣������ߵĶ���O����ˮƽ���ϣ��Գ�����ˮƽ��OC����A��B�������������ϣ��ҵ�A��ˮƽ��ľ���AC=4�ף���B��ˮƽ�����Ϊ2�ף�OC=8�ף�
��ͼ��ij�㳡��Ƶ�һ���������͵��ݽ����������ߵ�һ���֣������ߵĶ���O����ˮƽ���ϣ��Գ�����ˮƽ��OC����A��B�������������ϣ��ҵ�A��ˮƽ��ľ���AC=4�ף���B��ˮƽ�����Ϊ2�ף�OC=8�ף����� ��1������������Խ������ʵ�ƽ��ֱ������ϵ���Ӷ�������������ߵĽ���ʽ��
��2����������֮���߶���࣬������Ӧ��ͼ�Σ�д���������ɣ�
��3������ǰ�������ϵ�������߽���ʽ������õ�B�����꣬�ٸ������������ƿ����������֧��������ʡʱ��O��P֮��ľ��룬ע��˴�ֻд���𰸼��ɣ�
��� 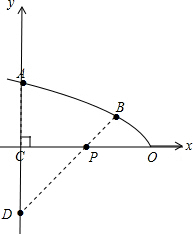 �⣺��1������ͼ��ʾ��
�⣺��1������ͼ��ʾ��
������ɵã���C������Ϊ��0��0������A������Ϊ��0��4������O������Ϊ��8��0����
��������ߵĽ���ʽΪ��x=ay2+8��
��0=a��42+8��
��ã�a=-$\frac{1}{2}$��
�������ߵĽ���ʽΪ��x=-$\frac{1}{2}$y2+8��
��2������A���ڵ�C�ĶԳƵ��D������DB��x�ύ�ڵ�P�����P��Ϊ����
��3������֧��������ʡʱ��O��P֮��ľ�����4�ף�
���� ���⿼����κ�����Ӧ�ã�����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ���������������ν�ϵ�˼�������⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
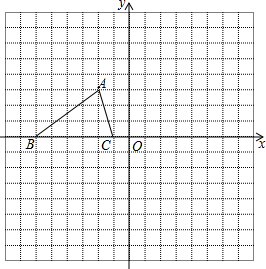 ��ͼ����֪��ABC��������������ΪA��-2��3����B��-6��0����C��-1��0����
��ͼ����֪��ABC��������������ΪA��-2��3����B��-6��0����C��-1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢ڢ� | C�� | �٢� | D�� | �٢ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com