
 如图,在平面直角坐标系中,O是原点,直线y=$\frac{3}{4}$x-3分别交x轴、y轴于点A、点C,点B在y轴正半轴上,且OB=OA.点D(2,m)在直线AB上,点P是x轴上的一个动点,设点P的横坐标为t.
如图,在平面直角坐标系中,O是原点,直线y=$\frac{3}{4}$x-3分别交x轴、y轴于点A、点C,点B在y轴正半轴上,且OB=OA.点D(2,m)在直线AB上,点P是x轴上的一个动点,设点P的横坐标为t.分析 (1)首先求出A、B两点坐标,利用待定系数法即可解决问题.
(2)由题意S△APB-S△DPA=$\frac{1}{4}$•S△ABC,可得$\frac{1}{2}$•|4-t|•4-$\frac{1}{2}$|4-t|•2=$\frac{1}{4}$•$\frac{1}{2}$•7•4,解方程即可.
(3)分两种情形求解①如图2中,以PD为斜边的等腰直角三角形的直角顶点为E或E′,当点E在AB边上时,易知DP⊥OA.②如图3中,当E′在AC边上时,作E′G⊥OP于G,EH⊥OP于H,连接OD、OE′、AE.想办法求出点E′的坐标,利用待定系数法即可解决问题.
解答 解:(1)∵直线y=$\frac{3}{4}$x-3分别交x轴、y轴于点A、点C,
∴A(4,0),C(-3,0),
∴OA=4,OC=3,
∵OB=OA=4,
∴B(4,0),
设直线AB的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=-x+4.
(2)如图1中,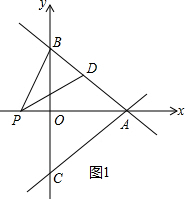
∵点D(2,m)在直线AB上,
∴m=-2+4=2,
∴D(2,2),
由题意△BDP的面积等于△ABC面积的$\frac{1}{4}$,
∴S△APB-S△DPA=$\frac{1}{4}$•S△ABC,
∴$\frac{1}{2}$•|4-t|•4-$\frac{1}{2}$|4-t|•2=$\frac{1}{4}$•$\frac{1}{2}$•7•4,
解得t=$\frac{15}{2}$或$\frac{1}{2}$.
(3)①如图2中,以PD为斜边的等腰直角三角形的直角顶点为E或E′,当点E在AB边上时,易知DP⊥OA.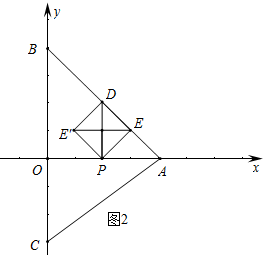
∵BD=AD,DP∥OB,
∴OP=PA=2,
∴P(2,0).
∴t=2.
②如图3中,当E′在AC边上时,作E′G⊥OP于G,EH⊥OP于H,连接OD、OE′、AE.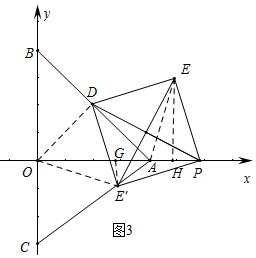
∵∠ODA=∠EDE′=90°,
∴∠ODE′=∠ADE,
在∠ODE′和△ADE中,
$\left\{\begin{array}{l}{DO=DA}\\{∠ODE′=∠ADE}\\{DE′=DE}\end{array}\right.$,
∴△ODE′≌△ADE,
∴OE′=AE,
易证△PEH≌△E′PG,
∴GE′=PH,EH=PG,
∵∠GOE′=∠DOE′-45°,∠OAE=∠90°+∠AEH,
∠OAE=45°+∠DAE=45°+∠DOE′,
∴∠AEH=∠DOE′-45°,
∴∠E′OG=∠AEH,
∵OE′=EH,∠OGE′=∠AHE=90°,
∴△OGE′≌△EHA,
∴OG=EH=PG=$\frac{1}{2}$t,GE′=AH=PH=$\frac{1}{2}$(t-4),
∴E′[$\frac{1}{2}$t,-$\frac{1}{2}$(t-4)],
∵点E′在直线AC时,直线AC的解析式为y=$\frac{3}{4}$x-3,
∴-$\frac{1}{2}$(t-4)=$\frac{3}{4}$×$\frac{1}{2}$t-3,
∴t=$\frac{40}{7}$,
综上所述,t=2或$\frac{40}{7}$时,点E落在△ABC的边上.
点评 本题考查一次函数的应用、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
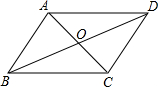 如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )| A. | AB=AD,BC=CD | B. | AO=OC,BO=DO | C. | AO⊥OD | D. | AO⊥AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a是实数,则|a|≥0 | B. | 在地球上,抛出的篮球会落下 | ||
| C. | 打开电视机,正在播放广告 | D. | 从装有黑球,白球的袋里摸出红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
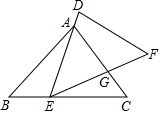 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AD}{AE}$=$\frac{GF}{GE}$ | C. | $\frac{AG}{AC}$=$\frac{EG}{EF}$ | D. | $\frac{ED}{EF}$=$\frac{EG}{EA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
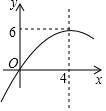 已知抛物线y=ax2+bx+c的图象如图所示,顶点为(4,6),则下列说法错误的是( )
已知抛物线y=ax2+bx+c的图象如图所示,顶点为(4,6),则下列说法错误的是( )| A. | b2>4ac | B. | ax2+bx+c≤6 | ||
| C. | 若点(2,m)(5,n)在抛物线上,则m>n | D. | 8a+b=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 4 | D. | 4或-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com