
【题目】在某市实施城中村改造的过程中,“旺鑫”拆迁工程队承包了一项10000 m2的拆迁工程.由于准备工作充分,实际拆迁效率比原计划提高了25%,提前2天完成了任务,请解答下列问题:
(1)求“旺鑫”拆迁工程队现在平均每天拆迁多少平方米;
(2)为了尽量减少拆迁给市民带来的不便,在拆迁工作进行了2天后,“旺鑫”拆迁工程队的领导决定加快拆迁工作,将余下的拆迁任务在5天内完成,那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少平方米?
【答案】(1)“旺鑫”拆迁工程队现在平均每天拆迁1250 m2;(2)“旺鑫”拆迁工程队平均每天至少再多拆迁250m2.
【解析】
(1)设“旺鑫”折迁工程队计划平均每天折迁![]()
![]() ,根据它们速率提高前后的时间差为
,根据它们速率提高前后的时间差为![]() 天列出方程并解答;
天列出方程并解答;
(2)设“旺鑫”折迁工程队现在平均每天折迁![]()
![]() ,根据工作时间必须在
,根据工作时间必须在![]() 天内完成列出不等式并解答.
天内完成列出不等式并解答.
(1)设“旺鑫”拆迁工程队计划平均每天拆迁x m2.
由题意,得![]() ﹣
﹣![]() =2,
=2,
解得x=1000,
经检验,x=1000是原方程的解并符合题意.
(1+25%)×1000=1250(m2).
答:设“旺鑫”拆迁工程队现在平均每天拆迁1250 m2.
(2)设“旺鑫”拆迁工程队现在平均每天拆迁y m2.
由题意,得5(1250+y)≥10000﹣2×1250
解得y≥250.
答:“旺鑫”拆迁工程队平均每天至少再多拆迁250m2.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,CD是△ABC的角平分线,若在边BC上截取CE=CB,连接DE,则图中等腰三角形有( )

A.3个B.4个C.5个D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2,0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2>![]() ﹣1;以上结论中正确结论的序号为 .
﹣1;以上结论中正确结论的序号为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
求证:AD平分∠BAC,填写分析和证明中的空白.

证明:∵AD⊥BC,EF⊥BC(已知)
∴______∥______(______)
∴______=______(两直线平行,内错角相等)
______=______(两直线平行,同位角相等)
∵______(已知),∴______
即AD平分∠BAC(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,则:
,则:
①线段PB= ,PC= ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足![]() ,求
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )

A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
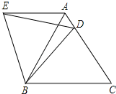
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com