练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

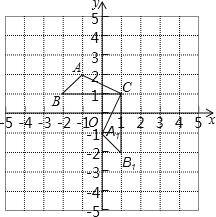
    【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（﹣1，2）、B（﹣2，1）、C（1，1）（正方形网格中每个小正方形的边长是1个单位长度）．

    （1）△A1B1C1是△ABC绕点 逆时针旋转 度得到的，B1的坐标是 ；

    （2）求出线段AC旋转过程中所扫过的面积（结果保留π）．

    【答案】（1）C 90 （1，-2）；（2） .

    【解析】

    试题分析：（1）由图可知旋转中心是点C，∠BCB1=90°，∴旋转角是90度.通过数格子发现B1的坐标；（2）线段AC扫过的图形是以C为圆心，AC为半径，圆心角为90的扇形，根据扇形面积计算公式可求得面积.

    试题解析：（1）△A1B1C1是△ABC绕点C逆时针旋转90度得到的，B1的坐标是：（1，﹣2）；（2）线段AC旋转过程中所扫过的面积为以点C为圆心，AC为半径的扇形的面积．∵，∴面积为：，即线段AC旋转过程中所扫过的面积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列四个命题中，错误的是 ( )

    A.直径是弦B.弦是直径C.同圆的直径都相等D.圆中最长的弦是直径

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．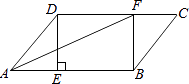

    （1）求证：四边形BFDE是矩形；
    （2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

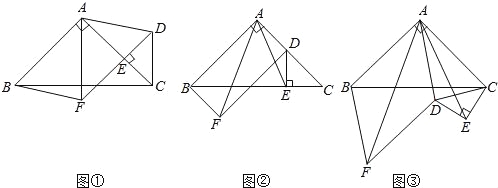
    【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．

    （1）请直接写出线段AF，AE的数量关系 ；

    （2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；

    （3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

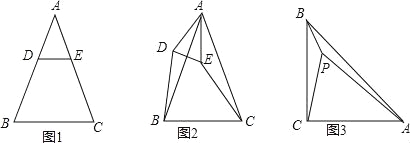
    【题目】已知△ABC是等腰三角形，AB=AC．

    （1）特殊情形：如图1，当DE∥BC时，有DB EC．（填“＞”，“＜”或“=”）

    （2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．

    （3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a(c－1)＝c－1，a≠1，求c2－1的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，△ABC的角平分线OB与角平分线OC相交于点O，过点O作MN∥BC，分别交AB、AC于点M、N．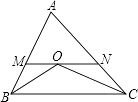

    （1）请写出图中所有的等腰三角形；
    （2）若AB+AC=14，求△AMN的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽，他为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成．将图中正方形MNKT，正方形EFGH，正方形ABCD的面积分别记为S1 ， S2 ， S3 ， 若S1+S2+S3=18，则正方形EFGH的面积为（ ）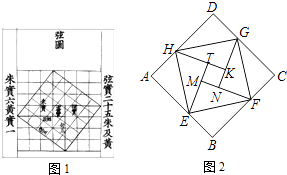

    A.9
    B.6
    C.5
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016湖北襄阳第23题)

    襄阳市某企业积极响应政府“创新发展”的号召，研发了一种新产品．已知研发、生产这种产品的成本为30元／件，且年销售量y(万件)关于售价x(元／件)的函数解析式为：

    (1)若企业销售该产品获得自睥利润为W(万元)，请直接写出年利润W(万元)关于售价(元/件)的函数解析式；

    (2)当该产品的售价x(元/件)为多少时，企业销售该产品获得的年利润最大?最大年利润是多少?

    (3)若企业销售该产品的年利澜不少于750万元，试确定该产品的售价x(元/件)的取值范围．

    查看答案和解析>>

    同步练习册答案