
【题目】有甲、乙两位同学,根据“关于x的一元二次方程kx2﹣(k+2)x+2=0”(k为实数)这一已知条件,他们各自提出了一个问题考查对方,问题如下:
甲:你能不解方程判断方程实数根的情况吗?
乙:若方程有两个不相等的正整数根,你知道整数k的值等于多少吗?请你帮助两人解决上述问题.
【答案】见解析.
【解析】试题分析:(1)首先根据一元二次方程的定义得出k≠0,再计算△=(k+2)2-4k×2=(k-2)2≥0,由判别式的意义即可判定方程有实数根;
(2)利用因式分解法求出方程的两根为x1=1,x2=![]() ,根据方程有两个不相等的正整数根,得出整数k=1.
,根据方程有两个不相等的正整数根,得出整数k=1.
试题解析:(1)∵kx2﹣(k+2)x+2=0(k为实数)是关于x的一元二次方程,
∴k≠0,
∵△=(k+2)2﹣4k×2=(k﹣2)2≥0,
∴方程有实数根;
(2)kx2﹣(k+2)x+2=0,
(x﹣1)(kx﹣2)=0,
x﹣1=0,或kx﹣2=0,
解得x1=1,x2=![]() ,
,
∵方程有两个不相等的正整数根,且k为整数,
∴k=1或2,
∵k=2时,x1=x2=1,两根相等,不合题意舍去,
∴k=1.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】每年农历五月初五,是中国民间的传统节日——端午节.它始于我国的春秋战国时期,已列为世界非物质文化遗产.时至今日,端午节在我国仍是一个十分盛行的节日.今年端午节,某地甲、乙两家超市为吸引更多的顾客,开展促销活动,对某种质量和售价相同的粽子分别推出了不同的优惠方案.甲超市的方案是:购买该种粽子超过80元后,超出80元的部分按九折收费;乙超市的方案是:购买该种粽子超过120元后,超出120元的部分按八折收费.请根据顾客购买粽子的金额,选择到哪家超市购买粽子划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为( )
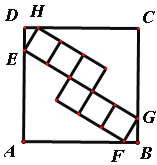
A.6 B.5 C.2![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
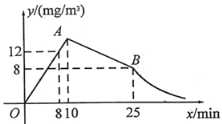
【题目】春季是流感高发的季节,为此,某校为预防流感,对教室进行熏药消毒.在对教室进行消毒的过程中,先经过10min的药物燃烧,再封闭教室15min,然后打开门窗进行通风.已知室内空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系式如图所示(即图中线段OA、线段AB和双曲线在点B及其右侧部分),请根据图中信息解答下列问题:
之间的函数关系式如图所示(即图中线段OA、线段AB和双曲线在点B及其右侧部分),请根据图中信息解答下列问题:
(1)求药物燃烧阶段和打开门窗进行通风阶段![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若室内空气中的含药量不低于![]() 且持续时间不少于35min,才能有效消灭病毒,则此次消毒是否有效?请说明理由.
且持续时间不少于35min,才能有效消灭病毒,则此次消毒是否有效?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)用方程解答下列问题
(1)一个角的余角比它的补角的![]() 还少15°,求这个角的度数.
还少15°,求这个角的度数.
(2)几个人共同搬运一批货物,如果每人搬运8箱货物,则剩下7箱货物未搬运;如果每人搬运12箱货物,则缺13箱货物,求参与搬运货物的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究逼近![]() 的有理近似值.
的有理近似值.
方法介绍:
经过![]() 步操作(
步操作(![]() 为正整数)不断寻找有理数
为正整数)不断寻找有理数![]() ,
,![]() ,使得
,使得![]() ,并且让
,并且让![]() 的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小
的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小![]() 对应的点
对应的点![]() 所在线段的长度(二分法)
所在线段的长度(二分法)
思路
在数轴上记![]() ,
,![]() 对应的点分别为
对应的点分别为![]() ,
,![]() 和
和![]() 的平均数
的平均数![]() 对应线段
对应线段![]() 的中点(记为
的中点(记为![]() ).通过判断
).通过判断![]() 还是
还是![]() ,得到点
,得到点![]() 是在二等分后的“左线段
是在二等分后的“左线段![]() ”上还是“右线段
”上还是“右线段![]() ”上,重复上述步骤,不断得到
”上,重复上述步骤,不断得到![]() ,从而得到
,从而得到![]() 更精确的近似值.
更精确的近似值.
具体操作步骤及填写“阅读活动任务单”:
(1)当![]() 时,
时,
①寻找左右界值:先寻找两个连续正整数![]() ,使得
,使得![]() .
.
因为![]() ,所以
,所以![]() ,那么
,那么![]() ,
,![]() ,线段
,线段![]() 的中点
的中点![]() 对应的数
对应的数![]() .
.
②二分定位:判断点![]() 在“左线段
在“左线段![]() ”上还是在“右线段
”上还是在“右线段![]() ”上.
”上.
比较7与![]() 的大小,从而确定
的大小,从而确定![]() 与
与![]() 的大小;
的大小;
因为![]() >
> ![]() (填 “>”或“<”),得到点
(填 “>”或“<”),得到点![]() 在线段
在线段 ![]() 上(填“
上(填“![]() ”或“
”或“![]() ”).
”).
(2)当![]() 时,在(1)中所得
时,在(1)中所得![]() 的基础上,仿照以上步骤,继续进行下去,得到表中
的基础上,仿照以上步骤,继续进行下去,得到表中![]() 时的相应内容.
时的相应内容.
请继续仿照以上步骤操作下去,补全“阅读活动任务单”:
|
|
|
|
| 点 | 得出更精确的 |
1 | 2 | 3 | 2.5 |
| 点 |
|
2 | 2.5 | 3 | 2.75 |
| 点 |
|
3 | 2.5 | 2.75 | 2.625 |
| ||
4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
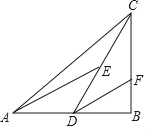
【题目】定义:有两条边长的比值为![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出![]() 的值为 ;
的值为 ;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.

(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数表达式,并写出自变量的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com