Question

9．如图，正三角形ABC和正三角形DCE的边BC和CE在同一直线上（如图1），已知：AD=BE，AD、BE成60°角．
（1）当正三角形ABC绕顶点C旋转至图2和图3（B、C、D共线）位置时，AD和BE的关系是否发生变化，为什么？
（2）试判断图3中，△MNC的形状，并说明理由．

Answer 1

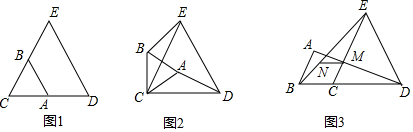
分析 （1）图2，DA和EB的延长线相交于H，利用等边三角形的性质得CB=CA，CE=CD，∠BCA=∠ECD=60°，则∠BCE=∠ACD，于是可证明△BCE≌△ACD，所以BE=AD，∠BEC=∠ADC，然后利用三角形内角和可得到∠EHD=∠ECD=60°，即AD、BE成60°角；在图3中，同样方法得到△BCE≌△ACD，则BE=AD，∠BEC=∠ADC，∠DOE=∠ECD=60°，即AD、BE成60°角；
（2）通过证明△CDM≌△CEN得到CM=CN，则根据等边三角形的判定方法可判断△CMN为等边三角形．

解答 解：（1）AD和BE的关系不发生变化．理由如下：
图2，DA和EB的延长线相交于H，
∵△ABC和△DCE为等边三角形，
∴CB=CA，CE=CD，∠BCA=∠ECD=60°，
∴∠BCA-∠ECA=∠ECD-∠ECA，即∠BCE=∠ACD，
在△BCE和△ACD中
$\left\{\begin{array}{l}{CB=CA}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$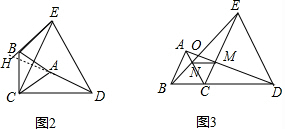
∴△BCE≌△ACD，
∴BE=AD，∠BEC=∠ADC，
∴∠EHD=∠ECD=60°，
即AD、BE成60°角；
图3，与图2一样可证明△BCE≌△ACD，
∴BE=AD，∠BEC=∠ADC，
∴∠DOE=∠ECD=60°，
即AD、BE成60°角；
（2）△MNC为等边三角形．理由如下：
∵∠ACB=60°，∠ECD=60°，
∴∠NCE=60°，
在△CDM和△CEN中
$\left\{\begin{array}{l}{∠DCM=∠ECN}\\{CD=CE}\\{∠CDM=∠CEN}\end{array}\right.$，
∴△CDM≌△CEN，
∴CM=CN，
∴△CMN为等边三角形．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的性质和全等三角形的判定与性质．