
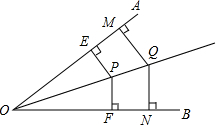
 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.  新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
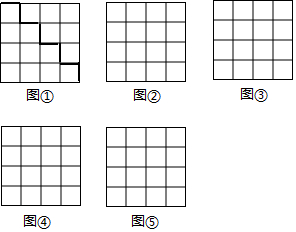 如图(1),把大小为4×4的正方形方格图形分割成两个全等图形,请在图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.
如图(1),把大小为4×4的正方形方格图形分割成两个全等图形,请在图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
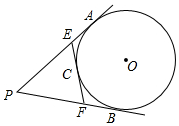 如图,PA,PB是圆O的切线,切点为分别A,B,圆O的切线EF分别交PA,PB于点E,F,切点C在弧$\widehat{AB}$上,若PA长为2,则△PEF的周长是4.
如图,PA,PB是圆O的切线,切点为分别A,B,圆O的切线EF分别交PA,PB于点E,F,切点C在弧$\widehat{AB}$上,若PA长为2,则△PEF的周长是4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com