
如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△![]() POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.

解:(1)把A(1,-4)代入y=kx-6,得k=2,∴y=2x-6,∴B(3,0).
∵A为顶点,![]() ∴设抛物线的解析为y=a(x-1)2-4,解得a=1,
∴设抛物线的解析为y=a(x-1)2-4,解得a=1,
∴y=(x-1)2-4=x2-2x-3
(2)存在.∵OB=OC=3,OP=OP,∴当∠POB=∠POC时,△POB≌△POC,
 此时PO平分第三象限,即PO的解析式为y=-x.
此时PO平分第三象限,即PO的解析式为y=-x.
设P(m,-m),则-m=m2-2m-3,解得m=![]() (m=
(m=![]() >0,舍),
>0,舍),
∴P(![]() ,
,![]() ).
).
(3)①如图,当∠Q1AB=90°时,△DAQ1∽△DOB,
∴![]() ,即
,即![]() ,∴DQ1=
,∴DQ1=![]() ,
,
∴OQ1=![]() ,即Q1(0,
,即Q1(0,![]() );
);
②如图,当∠Q2BA=90°时,△BOQ2∽△DOB,
∴![]() ,即
,即![]() ,
,
∴OQ2=![]() ,即Q2(0,
,即Q2(0,![]() );
);
③如图,当∠AQ3B=90°时,作AE⊥y轴于E,
则△BOQ3∽△Q3EA,
∴![]() ,即
,即![]() ,
,
∴OQ32-4OQ3+3=0,∴OQ3=1或3,
即Q3(0,-1),Q4(0,-3).
综上,Q点坐标为(0,![]() )或(0,
)或(0,![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).


科目:初中数学 来源: 题型:
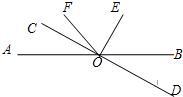 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.查看答案和解析>>
科目:初中数学 来源: 题型:
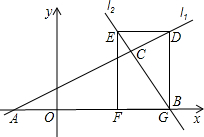 如图,已知直线l1:y=
如图,已知直线l1:y=| 2 |
| 3 |
| 8 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com