
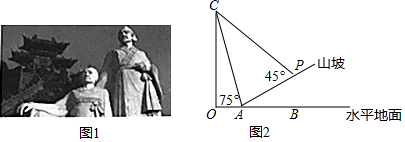
分析 过点P作PE⊥OB于点E,PF⊥OC于点F,设PE=x,则AE=3x,在Rt△AEP中根据勾股定理可得PE=$\sqrt{10}$,则AE=3$\sqrt{10}$,设CF=PF=m米,则OC=(m+$\sqrt{10}$)米、OA=(m-3$\sqrt{10}$)米,在Rt△AOC中,由tan75°=$\frac{OC}{OA}$求得m的值,继而可得答案.
解答 解:过点P作PE⊥OB于点E,PF⊥OC于点F,
∵i=1:3,AP=10,
设PE=x,则AE=3x,
在Rt△AEP中,x2+(3x)2=102,
解得:x=$\sqrt{10}$或x=-$\sqrt{10}$(舍),
∴PE=$\sqrt{10}$,则AE=3$\sqrt{10}$,
∵∠CPF=∠PCF=45°,
∴CF=PF,
设CF=PF=m米,则OC=(m+$\sqrt{10}$)米,OA=(m-3$\sqrt{10}$)米,
在Rt△AOC中,tan75°=$\frac{OC}{OA}$=$\frac{m+\sqrt{10}}{m-3\sqrt{10}}$,即m+$\sqrt{10}$=tan75°•(m-3$\sqrt{10}$),
解得:m≈14.3,
∴OC=14.3+$\sqrt{10}$≈17.5米,
答:塑像的高度约为17.5米.
点评 此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.


科目:初中数学 来源: 题型:填空题
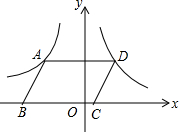 如图,在平面直角坐标系中,?ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=-$\frac{3}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象上,则?ABCD的面积为4.
如图,在平面直角坐标系中,?ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=-$\frac{3}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象上,则?ABCD的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
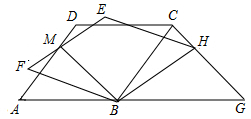 如图,菱形ABCD边长为5,tan∠DAB=$\frac{4}{3}$,将菱形绕点B按顺时针方向旋转角α(0°<α<∠DBA)得到菱形FBHE(点A的对应点为点F),EF与AD交于点M,连接BM.
如图,菱形ABCD边长为5,tan∠DAB=$\frac{4}{3}$,将菱形绕点B按顺时针方向旋转角α(0°<α<∠DBA)得到菱形FBHE(点A的对应点为点F),EF与AD交于点M,连接BM.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 9 | C. | 13 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 投资量x(万元) | 2 |
| 种植树木利润y1(万元) | 4 |
| 种植花卉利润y2(万元) | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com