
【题目】在推进城乡生活垃圾分类的行动中,为了了解社区居民对垃圾分类知识的掌握情况,某社区随机抽取40名居民进行测试,并对他们的得分数据进行收集、整理、描述和分析.下面给出了部分信息:
a.社区40名居民得分的频数分布直方图:(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100):
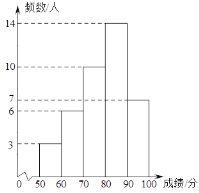
b.社区居民得分在80≤x<90这一组的是:
80 80 81 82 83 84 84 85 85 85 86 86 87 89
c.40个社区居民的年龄和垃圾分类知识得分情况统计图:
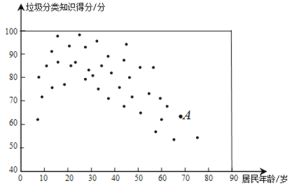
d.社区居民甲的垃圾分类知识得分为89分.
根据以上信息,回答下列问题:
(1)社区居民甲的得分在抽取的40名居民得分中从高到低排名第 ;
(2)在垃圾分类得分比居民甲得分高的居民中,居民年龄最大约是 岁;
(3)下列推断合理的是 .
①相比于点A所代表的社区居民,居民甲的得分略高一些,说明青年人比老年人垃圾分类知识掌握得更好一些;
②垃圾分类知识得分在90分以上的社区居民年龄主要集中在15岁到35岁之间,说明青年人垃圾分类知识掌握更为全面,他们可以向身边的老年人多宣传垃圾分类知识.
【答案】(1)8;(2)45;(3)②.
【解析】
(1)由题意根据90≤x<100的人数有7人,即可判断;
(2)根据题意直接利用图2中信息判断即可;
(3)根据题意直接利用图2中信息进行分析判断即可.
解:(1)∵90≤x<100的人数有7人,
∴89分又是80≤x<90中的最高分,
∴89分是第8名,
故答案为:8.
(2)观察图2可知,在垃圾分类得分比居民甲得分高的居民中,居民年龄最大约是45岁.
故答案为:45.
(3)观察图象可知:垃圾分类知识得分在90分以上的社区居民年龄主要集中在15岁到35岁之间,说明青年人垃圾分类知识掌握更为全面,他们可以向身边的老年人多宣传垃圾分类知识.
故②正确.
故答案为:②.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图2中阴影部分的周长与图1中阴影部分的周长的差为l,若要知道l的值,只要测量图中哪条线段的长( )
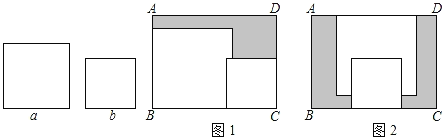
A.aB.bC.ADD.AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(![]() )是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限送一项),下面是根据调查结果绘制出不完整的两个统计图表:
)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限送一项),下面是根据调查结果绘制出不完整的两个统计图表:
生活信息关注度条形统计图
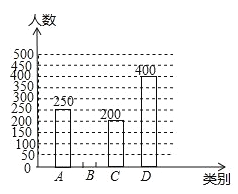
A:政府服务信息 B:城市医疗信息 C:交于资源信息 D:交通信息
生活信息关注度扇形统计图
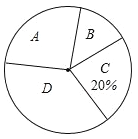
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是______,扇形统计图中![]() 部分的圆心角的度数是_______.并补全条形统计图;
部分的圆心角的度数是_______.并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是_______类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
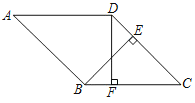
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
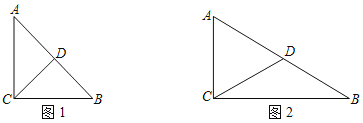
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与y轴交于点A,与抛物线
的图象与y轴交于点A,与抛物线![]() 的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
(1)求出抛物线的对称轴和点C坐标;
(2)①当![]() 时,直接写出抛物线
时,直接写出抛物线![]() 与图形G的公共点个数.
与图形G的公共点个数.
②如果抛物线![]() 与图形G有且只有一个公共点,求出a的取值范围.
与图形G有且只有一个公共点,求出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程.
已知:![]() 中,
中,![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ,
,![]() 和
和![]() 交于点
交于点![]() ;
;
③连接![]() 和
和![]() ;
;
④以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() .
.
所以![]() .
.
根据小菲设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);

(2)完成下面的证明.

证明:连接![]()
∵![]() 和
和![]() 分别为
分别为![]() 、
、![]() 的垂直平分线,
的垂直平分线,
∴![]() ________.
________.
∴![]() 是
是![]() 的外接圆.
的外接圆.
∵点![]() 是
是![]() 上的一点,
上的一点,
∴![]() .(____________).(填推理的依据)
.(____________).(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,存在抛物线
中,存在抛物线![]() 以及两点
以及两点![]() .
.
(1)求该抛物线的顶点坐标;(用含![]() 的代数式表示)
的代数式表示)
(2)若该抛物线经过点![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)若该抛物线与线段![]() 有公共点,结合图象,求
有公共点,结合图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
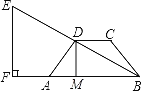
【题目】如图,在四边形ABCD中,AB∥DC,AD=BC,AB=10,CD=4,DM⊥AB于点M.连接BD并延长到E,使DE=BD,作EF⊥AB,交BA的延长线于点F.
(1)求MB的长;
(2)求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com