
(12分)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
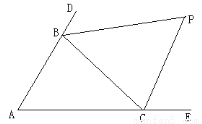
(1)若∠A=50°,则∠P= °;
(2)若∠A=90°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系,并说明理由。
【解析】
(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,∠DBC+∠BCE=360°-130°=230°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC= ∠DBC,∠PCB=
∠DBC,∠PCB= ∠ECB,
∠ECB,
∴∠PBC+∠PCB= (∠DBC+∠ECB)=115°,
(∠DBC+∠ECB)=115°,
∴∠P=65°.
同理得:(2)45°;
(3)40°
(4)∠P=90°- ∠A.理由如下:
∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°+ ∠A
∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°- ∠A.
∠A.
【解析】
试题分析:(1)若∠A=50°,则有∠ABC+∠ACB=130°,∠DBC+∠BCE=360°-130°=230°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数;
(2)、(3)和(1)的解题步骤类似;(4)利用角平分线的性质和三角形的外角性质可求出∠BCP= (∠A+∠ABC),∠CBP=
(∠A+∠ABC),∠CBP= (∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
(∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
考点:三角形内角和定理;三角形的外角性质.


科目:初中数学 来源:2014-2015学年浙江省慈溪市八年级12月评估测试数学试卷(解析版) 题型:解答题
(本题10分)某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10 台和液晶显示器8台,共需要资金7000 元;若购进电脑机箱2台和液晶显示器5台, 共需要资金4120元.
(1)每合电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省慈溪市八年级12月评估测试数学试卷(解析版) 题型:选择题
从长为3cm,6cm,8cm,9cm的四条线段中任选三条线段,不能组成一个三角形的为( )
A.3cm,6cm,8cm B.3cm, 8cm,9cm
C.3cm,6cm,9cm D.6cm,8cm,9cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年新疆伊宁市八年级上学期期中考试数学试卷(解析版) 题型:选择题
△ABC中,∠C=90°,AD平分∠BAC交BC于点D,且CD=10cm,则点D到AB的距离是________。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年新疆伊宁市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,伊宁火车站附近现要建一个货物中转站,三条直线表示3条公路要求中转站到三条公路的距离相等,则可供选择的地址有( )
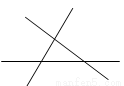
A.一处 B.两处 C.三处 D.四处
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安岳池白庙督导区八年级10月月考数学试卷(解析版) 题型:解答题
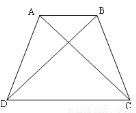
已知:如图DA=CB,∠ADC=∠BCD. 求证:∠ADB=∠BCA. (8分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com