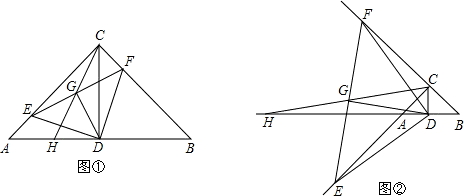
(1)证明:①如图①.
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠B=45°.
∵CD为边AB上的中线,
∴CD⊥AB,AD=CD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCB,
即∠A=∠DCF.
∵DF⊥DE,
∴∠ADE+∠EDC=90°,∠CDF+∠EDC=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
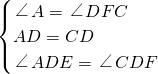
,
∴△AED≌△CFD(ASA),
∴AE=CF;
②∵在△ABC中,∠ACB=90°,G为EF的中点,
∴CG=

EF.
∵DF⊥DE,G为EF的中点,
∴GD=

EF.
∴CG=GD;
(2)解:①②还成立.
①AE=CF,证明如下:
如图②,∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°.
∵CD为边AB上的中线,
∴CD⊥AB,AD=CD=BD,∠ACD=∠BCD=45°,
∴∠EAD=∠180°-∠CAD=135°,∠FCD=180°-∠BCD=135°,
∴∠EAD=∠FCD.
∵DF⊥DE,
∴∠ADE+∠HDF=∠CDF+∠HDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
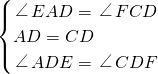
,
∴△AED≌△CFD(ASA),
∴AE=CF;
②CG=GD.证明如下:
Rt△EFC中,点G是EF边的中点,则CG=

EF.
在Rt△EFD中,点G是EF边的中点,则GD=

EF.
则CG=GD;
(3)解:AC=7或1,理由是:
∵AC=BC,CD是AB边上的中线,
∴CD⊥AB,
∴∠CDA=90°,
∴∠CHD+∠DCH=90°,∠CDG+∠HDG=90°,
∵由(1)知DG=CG,
∴∠CDG=∠GCD,
∴∠GDH=∠GHD,
∴DG=GH,
∴CG=GH=

CH=

×5=2.5,
∵∠EDF=90°,G为EF中点,
∴DG=

EF,
∴EF=5,
∵AE=3,
∴由(1)知AE=CF,
∴CF=3,
在Rt△ECF中,由勾股定理得:EC=

=4,
∴AC=AE+CE=3+4=7;
如图②,同理求出EF=5,CF=3,
在R△ECF中,根据勾股定理求出CE=4,
则AC=CE-AE=4-3=1,
综合上述:AC=7或1.
分析:(1)①通过全等三角形(△AED≌△CFD)的对应边相等证得AE=CF;
②根据Rt△ECF和Rt△EDF斜边上中线的性质来证明CG=GD;
(2)①②都成立.思路同(1);
(3)求出EF的长是5,在Rt△ECF中,CF=3,根据勾股定理求出EC,即可求出AC.
点评:本题考查了全等三角形的性质和判定,等腰直角三角形性质,直角三角形斜边上中线性质,勾股定理等知识点的综合运用,题目具有一定的代表性,证明过程类似.

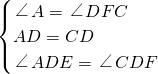 ,
, EF.
EF. EF.
EF.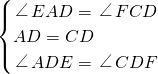 ,
, EF.
EF. EF.
EF. CH=
CH= ×5=2.5,
×5=2.5, EF,
EF, =4,
=4,

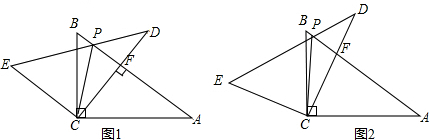
 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.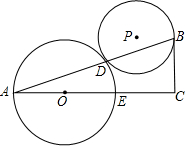 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,