
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
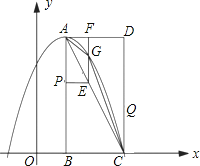
【答案】(1)点A的坐标为(1,4),抛物线的解析式为y=x2+2x+3;
(2)当t=2时,S△ACG的最大值为1;
(3)t的值为20-8![]() 或
或![]()
【解析】试题分析:(1)根据矩形的性质可以写出点A得到坐标;由顶点A的坐标可设该抛物线的顶点式方程为y=a(x-1)2+4,然后将点C的坐标代入,即可求得系数a的值(利用待定系数法求抛物线的解析式);(2)利用待定系数法求得直线AC的方程y=-2x+6;由图形与坐标变换可以求得点P的坐标(1,4-t),据此可以求得点E的纵坐标,将其代入直线AC方程可以求得点E或点G的横坐标;然后结合抛物线方程、图形与坐标变换可以求得GE=4-![]() 、点A到GE的距离为,C到GE的距离为2-
、点A到GE的距离为,C到GE的距离为2-![]() ;最后根据三角形的面积公式可以求得S△ACG=S△AEG+S△CEG=-
;最后根据三角形的面积公式可以求得S△ACG=S△AEG+S△CEG=-![]() (t-2)2+1,由二次函数的最值可以解得t=2时,S△ACG的最大值为1;(3)因为菱形是邻边相等的平行四边形,所以点H在直线EF上.
(t-2)2+1,由二次函数的最值可以解得t=2时,S△ACG的最大值为1;(3)因为菱形是邻边相等的平行四边形,所以点H在直线EF上.
试题解析:
(1)A(1,4).
由题意知,可设抛物线解析式为y=a(x1)2+4,
∵抛物线过点C(3,0),
∴0=a(31)2+4,
解得,a=1,
∴抛物线的解析式为y=(x1)2+4,即y=x2+2x+3.
(2)∵A(1,4),C(3,0),
∴可求直线AC的解析式为y=2x+6.
∵点P(1,4t).
∴将y=4t代入y=2x+6中,解得点E的横坐标为x=1+![]() .
.
∴点G的横坐标为1+![]() ,代入抛物线的解析式中,可求点G的纵坐标为4
,代入抛物线的解析式中,可求点G的纵坐标为4![]() .
.
∴GE=(4![]() )(4t)=t
)(4t)=t![]() .
.
又∵点A到GE的距离为![]() ,C到GE的距离为2
,C到GE的距离为2![]() ,
,
即S△ACG=S△AEG+S△CEG=![]() EG
EG![]() +
+![]() EG(2
EG(2![]() )
)
=![]() 2(t
2(t![]() )=
)=![]() (t2)2+1.
(t2)2+1.
当t=2时,S△ACG的最大值为1.
(3)第一种情况如图1所示,点H在AC的上方,由四边形CQEH是菱形知CQ=CE=t,
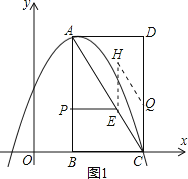
根据△APE∽△ABC,知
![]() ,即
,即![]() ,解得t=20
,解得t=20![]() ;
;
第二种情况如图2所示,
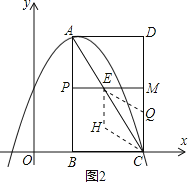
点H在AC的下方,由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE=![]() t,EM=2
t,EM=2![]() t,MQ=42t.
t,MQ=42t.
则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,即(2![]() t)2+(42t)2=t2,
t)2+(42t)2=t2,
解得,t1=![]() ,t2=4(不合题意,舍去).
,t2=4(不合题意,舍去).
综上所述,t=20![]() 或t=
或t=![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~100;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图1和如图2所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
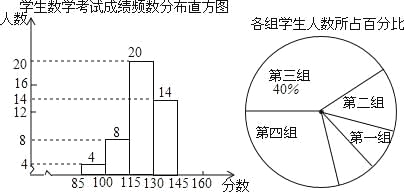
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1600名学生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组有两名女生和两名男生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h) 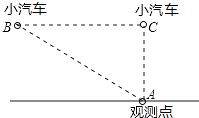
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A、B所表示的数分别是4,8,
(1)请用尺规作图的方法确定原点O的位置(不写做法,保留作图痕迹)
(2)已知动点M从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,同时点N从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
①运动1秒后,点M表示的数是_____,点N表示的数为______
②运动t秒后,点M表示的数是_____,点N表示的数为______
③若线段BN=2,求此时t的大小以及相应的M所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年遵义市固定资产总投资计划为2580亿元,将2580亿元用科学记数法表示为( )
A.2.58×1011
B.2.58×1012
C.2.58×1013
D.2.58×1014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com