
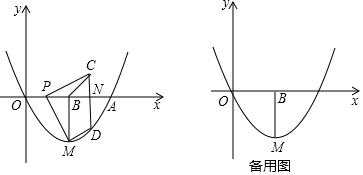
Ζ÷Έω Θ®1Θ©ΗυΨίΧβ“βœ»«σΒΟMΒΡΉχ±ξΘ§»ΜΚσΗυΨί¥ΐΕ®œΒ ΐΖ®Φ¥Ω…«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Ά®Ιΐ»ΐΫ«–Έ»ΪΒ»«σΒΟPB=CNΘ§BM=PNΘ§Ζ÷άύΧ÷¬έP‘ΎBΒψΒΡΉσ±Ώ”κ”“±ΏΘ§¥”Εχ«σΒΟCΒΡΉχ±ξΘΜ
Θ®3Θ©Ζ÷άύΧ÷¬έΒψP‘ΎOB…œ ±ΓΔOE…œ ±Θ§Α―CΒΡΚαΉχ±ξ¥ζ»κ≈ΉΈοœΏΒΡΫβΈω Ϋ«σΒΟDΒΡΉχ±ξΘ§»ΜΚσΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘±ΏœύΒ»Ν–≥ωΒ» ΫΘ§Ϋβ’βΗωΖΫ≥ΧΦ¥Ω…«σΒΟaΒΡ÷ΒΘ§ΫχΕχ«σΒΟPΒΡΉχ±ξΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©ΓΏΒψA”κΒψOΙΊ”ΎMBΕ‘≥ΤΘ§
Γύ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣx=4Θ°
”÷ΓΏMB=4Θ§
ΓύMΘ®4Θ§-4Θ©Θ°
ΫΪΒψAΚΆΒψMΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚ$\left\{\begin{array}{l}{64a+8b=0}\\{16a+4b=-4}\end{array}\right.$Θ§
ΫβΒΟΘΚa=$\frac{1}{4}$Θ§b=-2Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=$\frac{1}{4}$x2-2xΘ°
Θ®2Θ©ΓΏΓœMPB+ΓœBPC=90ΓψΘ§ΓœMPB+ΓœPMB=90ΓψΘ§
ΓύΓœCPB=ΓœPMBΘ°
‘ΎΓςMPBΚΆΓςPCN÷–$\left\{\begin{array}{l}{ΓœCPB=ΓœPMB}\\{ΓœMBP=ΓœCNP}\\{PC=CM}\end{array}\right.$
ΓύΓςMPBΓ’ΓςPCNΘ°
ΓύPB=CNΘ§PN=BM=4
ΓΏPΘ®aΘ§0Θ©Θ§OP=aΘ§«“ΒψP «œΏΕΈOE…œΒΡΕ·Βψ
ΓύPB=CN=|4-a|Θ§ON=|a+4|
ΔΌ»γΆΦ1Θ§Β±ΒψP‘ΎΒψBΉσ±Ώ ±Θ§ΒψC‘Ύx÷α…œΖΫΘ§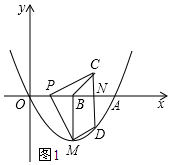
aΘΦ4Θ§4-aΘΨ0Θ§PB=CN=4-aΘ§
ΓύCΘ®a+4Θ§4-aΘ©
ΔΎ»γΆΦ2Θ§Β±ΒψP‘ΎΒψB”“±Ώ ±Θ§ΒψC‘Ύx÷αœ¬ΖΫΘ§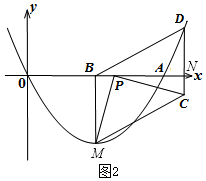
aΘΨ4Θ§4-aΘΦ0Θ§
ΓύPB=|4-a|=-Θ®4-aΘ©=a-4
ΓύCN=a-4
ΓύCΘ®a+4Θ§4-aΘ©
Ήέ…œΥυ ωΘ§ΒψCΉχ±ξ «CΘ®a+4Θ§4-aΘ©
Θ®3Θ©»γΆΦ1Υυ ΨΘ§Β±ΒψP‘ΎOB…œ ±Θ§
”…Θ®2Θ©Ω…÷ΣΒψCΒΡΉχ±ξΈΣΘ®a+4Θ§4-aΘ©Θ°
ΓΏΥΡ±Ώ–ΈBMDCΈΣΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύCD=BM=4Θ°
ΫΪx=a+4¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚy=$\frac{1}{4}$Θ®a+4Θ©2-2Θ®a+4Θ©=$\frac{1}{4}$a2-4Θ°
ΓύCD=4-a-Θ®$\frac{1}{4}$a2-4Θ©=4Θ§ΫβΒΟΘΚa=-2+2$\sqrt{5}$Μρa=-2-2$\sqrt{5}$Θ®…α»ΞΘ©Θ°
ΓύΒψPΒΡΉχ±ξΈΣΘ®-2+2$\sqrt{5}$Θ§0Θ©Θ°
»γΆΦ2Υυ ΨΘΚΒ±ΒψP‘ΎœΏΕΈBA…œ ±Θ°ΒψCΒΡΉχ±ξΈΣΘ®a+4Θ§4-aΘ©Θ§‘ρΒψDΒΡΉχ±ξΈΣΘ®a+4Θ§$\frac{1}{4}$a2-4Θ©
ΓύCD=$\frac{1}{4}$a2-4-Θ®4-aΘ©=4Θ°
ΫβΒΟΘΚa=-2+2$\sqrt{13}$Μρa=-2-2$\sqrt{13}$Θ®…α»ΞΘ©Θ°
ΓύΒψPΒΡΉχ±ξΈΣΘ®-2+2$\sqrt{13}$Θ§0Θ©Θ°
Ήέ…œΥυ ωΘ§ΒψPΒΡΉχ±ξΈΣΘ®-2+2$\sqrt{13}$Θ§0Θ©ΜρΘ®-2+2$\sqrt{5}$Θ§0Θ©Θ°
ΒψΤά ±ΨΧβΉ≈÷ΊΩΦ≤ιΝΥ¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΫβΈω ΫΓΔΆΦ–Έ–ΐΉΣ±δΜΜΓΔ»ΐΫ«–Έ»ΪΒ»ΒΡ≈–Ε®ΚΆ–‘÷ ΓΔΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΓΔΚ· ΐΆΦœσΒΡΫΜΒψΒΡ«σΖ®Θ§’“≥ωΆΦ–Έ÷–ΒΡ»ΪΒ»»ΐΫ«–ΈΘ§άϊ”Ο»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫœύΙΊœΏΕΈΒΡ≥ΛΕ» «Ϋβ¥πΈ ΧβΘ®2Θ©ΒΡΙΊΦϋΘ§“άΨίΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘±ΏœύΒ»Ν–≥ωΙΊ”ΎaΒΡΖΫ≥Χ «ΫβΧβΒΡΙΊΦϋΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2 | BΘ° | Γά2 | CΘ° | -2 | DΘ° | 16 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
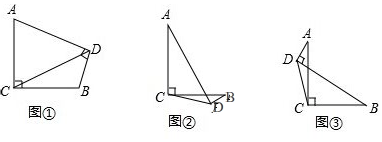
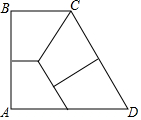 »γΆΦΘ§Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœA=90ΓψΘ§Υϋ«ΓΚΟΡήΑ¥ΆΦ ΨΖΫ Ϋ±ΜΖ÷Ην≥…ΥΡΗω»ΪΒ»ΒΡ÷±Ϋ«Χί–ΈΘ§‘ρABΘΚBC=$\sqrt{3}$ΘΚ1Θ°
»γΆΦΘ§Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœA=90ΓψΘ§Υϋ«ΓΚΟΡήΑ¥ΆΦ ΨΖΫ Ϋ±ΜΖ÷Ην≥…ΥΡΗω»ΪΒ»ΒΡ÷±Ϋ«Χί–ΈΘ§‘ρABΘΚBC=$\sqrt{3}$ΘΚ1Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -2 | BΘ° | -1 | CΘ° | 0 | DΘ° | 2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
 »γΆΦΘ§DEΓΆAB”ΎEΘ§DFΓΆAC”ΎFΘ§»τBD=CDΓΔBE=CFΘ§AB=6Θ§AC=10Θ§‘ρAE=8Θ°
»γΆΦΘ§DEΓΆAB”ΎEΘ§DFΓΆAC”ΎFΘ§»τBD=CDΓΔBE=CFΘ§AB=6Θ§AC=10Θ§‘ρAE=8Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
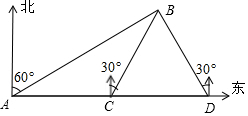 »γΆΦΘ§Ρ≥Μθ¬÷…œΈγ8 ±20Ζ÷¥”A¥Π≥ωΖΔΘ§¥Υ ±Ιέ≤βΒΫΚΘΒΚBΒΡΖΫΈΜΈΣ±±ΤΪΕΪ60ΓψΘ§ΗΟΜθ¬÷“‘ΟΩ–Γ ±30ΚΘάοΒΡΥΌΕ»œρΕΪΚΫ––ΒΫC¥ΠΘ§¥Υ ±Ιέ≤βΒΫΚΘΒΚBΒΡΖΫΈΜΈΣ±±ΤΪΕΪ30ΓψΘ§ΦΧ–χœρΕΪΚΫ––ΒΫD¥ΠΘ§Ιέ≤βΒΫΚΘΒΚBΒΡΖΫΈΜΈΣ±±ΤΪΈς30ΓψΘ°Β±Μθ¬÷ΒΫ¥οC¥Π ±«ΓΚΟ”κΚΘΒΚBœύΨύ60ΚΘάοΘ§«σΗΟΜθ¬÷ΒΫΒΫ¥οCΘ§D¥ΠΒΡ ±ΦδΘ°
»γΆΦΘ§Ρ≥Μθ¬÷…œΈγ8 ±20Ζ÷¥”A¥Π≥ωΖΔΘ§¥Υ ±Ιέ≤βΒΫΚΘΒΚBΒΡΖΫΈΜΈΣ±±ΤΪΕΪ60ΓψΘ§ΗΟΜθ¬÷“‘ΟΩ–Γ ±30ΚΘάοΒΡΥΌΕ»œρΕΪΚΫ––ΒΫC¥ΠΘ§¥Υ ±Ιέ≤βΒΫΚΘΒΚBΒΡΖΫΈΜΈΣ±±ΤΪΕΪ30ΓψΘ§ΦΧ–χœρΕΪΚΫ––ΒΫD¥ΠΘ§Ιέ≤βΒΫΚΘΒΚBΒΡΖΫΈΜΈΣ±±ΤΪΈς30ΓψΘ°Β±Μθ¬÷ΒΫ¥οC¥Π ±«ΓΚΟ”κΚΘΒΚBœύΨύ60ΚΘάοΘ§«σΗΟΜθ¬÷ΒΫΒΫ¥οCΘ§D¥ΠΒΡ ±ΦδΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
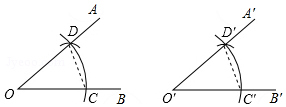
| AΘ° | ±ΏΫ«±Ώ | BΘ° | ±Ώ±Ώ±Ώ | CΘ° | Ϋ«±ΏΫ« | DΘ° | Ϋ«Ϋ«±Ώ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com