
【题目】如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A= ![]() ,BD是AC边上的中线.求:
,BD是AC边上的中线.求: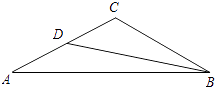
(1)△ABC的面积;
(2)∠ABD的余切值.
【答案】
(1)解:如图,过点C作CE⊥AB与点E,
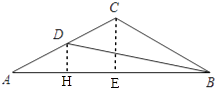
∴BE=BCcos∠ABC=8× ![]() =4
=4 ![]() ,
,
CE=BCsin∠ABC=8× ![]() =4,
=4,
在Rt△ACE中,∵sin∠A= ![]() ,
,
∴AC= ![]() =
= ![]() =4
=4 ![]() ,
,
∴AE= ![]() =
= ![]() =8,
=8,
则AB=AE+BE=8+4 ![]() ,
,
故S△ABC= ![]() ABCE=
ABCE= ![]() ×(8+4
×(8+4 ![]() )×4=16+8
)×4=16+8 ![]()
(2)解:过点D作DH⊥AB与点H,
∵CE⊥AB,
∴DH∥CE,
又∵D是AC中点,
∴AH=HE= ![]() AE=4,DH=
AE=4,DH= ![]() CE=2,
CE=2,
∴在Rt△BDH中,cot∠ABD= ![]() =
= ![]() =2
=2 ![]() +2
+2
【解析】(1)过点C作CE⊥AB与点E,在Rt△BCE中,∵BC=8,∠ABC=30°, 解Rt△BCE得出,BE=BCcos∠ABC,CE=BCsin∠ABC,在Rt△ACE中,由sin∠A的值表示出AC的长,根据勾股定理得出AE的长,从而得出S△ABC;(2)过点D作DH⊥AB与点H,根据平行线的判定得出DH∥CE,再根据中位线得判定得出AH=HE =4,DH =2,在Rt△BDH中,得出cot∠ABD的值。
【考点精析】根据题目的已知条件,利用平行线的判定与性质和三角形中位线定理的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
查看答案和解析>>
科目:初中数学 来源: 题型:
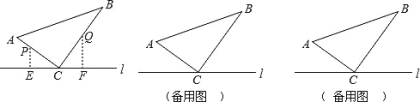
【题目】如图,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,![]() PEC 与
PEC 与![]() QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;
(2)请问:当 x 3 时,![]() PEC 与
PEC 与![]() QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发的960件新产品必须加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工48件产品的时间与乙工厂单独加工72件产品的时间相等,而且乙工厂每天比甲工厂多加工8件产品,在加工过程中,公司需每天支付50元劳务费请工程师到厂进行技术指导.
(1)甲、乙两个工厂每天各能加工多少件产品?
(2)该公司要选择既省时又省钱的工厂加工产品,乙工厂预计甲工厂将向公司报加工费用为每天800元,请问:乙工厂向公司报加工费用每天最多为多少元时,有望加工这批产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
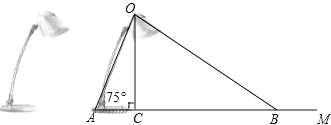
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com