
分析 根据二次根式的运算性质即可求出答案.
解答 解:(1)原式=2$\sqrt{3}$+$\frac{1}{3}$×3$\sqrt{3}$=3$\sqrt{3}$;
(2)原式=$\frac{2\sqrt{5}+\sqrt{5}}{\sqrt{5}}$-4=3-4=-1;
(3)原式=5$\sqrt{5}$-6$\sqrt{5}$-$\frac{\sqrt{5}}{5}$=-$\frac{6}{5}$$\sqrt{5}$;
(4)原式=4$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$+$\sqrt{2}$=$\frac{7}{2}$$\sqrt{2}$;
(5)原式=$\frac{\sqrt{15}}{5}$-$\frac{\sqrt{15}}{3}$=-$\frac{2\sqrt{15}}{15}$;
(6)原式=4×2-9=-1;
(7)原式=(3$\sqrt{2}$)2-2×3$\sqrt{2}$×$\sqrt{7}$+($\sqrt{7}$)2=25-6$\sqrt{14}$;
(8)原式=$\sqrt{36}$+10+$\sqrt{5}$-2=6+10+$\sqrt{5}$-2=14+$\sqrt{5}$;
(9)原式=$\frac{3\sqrt{2}×\sqrt{6}}{\sqrt{3}}$=3×2=6.
点评 本题考查二次根式的混合运算,涉及二次根式的运算性质,属于基础题型.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12(x-y)}{15(x+y)}$ | B. | $\frac{{y}^{2}-{x}^{2}}{x+y}$ | ||
| C. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}y+x{y}^{2}}$ | D. | $\frac{{x}^{2}-{y}^{2}}{(x+y)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
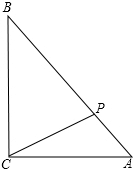 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com