
【题目】如图所示,已知△ABC,分别以AB、AC边作图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,下列结论①△AEC≌△ABF,②EC=FB,③EC⊥FB,④MA平分∠EMF中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】∵AE⊥AB,AF⊥AC,
∴∠EAB=∠FAC=90°,
∴∠EAB+∠BAC=∠FAC+∠BAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中

∴△AEC≌△ABF(SAS);
故①正确;
∵△AEC≌△ABF(已证)
∴EC=FB;
故②正确;
∵△AEC≌△ABF,
∴∠ACE=∠AFB,
∵∠FAC=90°,
∴∠AFB+∠AOF=90°,
∴∠ACE+∠AOF=90°,
∵∠AOF=∠COM,
∴∠ACE+∠COM=90°,
∴∠CMF=180°-90°=90°,
∴EC⊥BF;
故③正确;
作AP⊥CE于P,AQ⊥BF于Q,如图所示:

∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等).
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.
故④正确;
综合上述可得:①②③④共计4个正确.
故选D.


科目:初中数学 来源: 题型:
【题目】某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个零件,则可以超额完成5个,问:规定时间是多少?设规定时间为x小时,则可列方程为( )
A.38x﹣15=42x+5
B.38x+15=42x﹣5
C.42x+38x=15+5
D.42x﹣38x=15﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4 ,tan∠AEB=,AB∶BC=2∶3,求圆的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=3x2的图象向左平移2个单位,得到新的图象的二次函数表达式是( )
A.y=3x2+2
B.y=(3x+2)2
C.y=3(x+2)2
D.y=3(x﹣2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在暑假到来之前,某机构向八年级学生推荐了A,B,C三条游学线路,现对全级学生喜欢哪一条游学线路作调查,以决定最终的游学线路,下面的统计量中最值得关注的是( )
A. 方差 B. 平均数 C. 中位数 D. 众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:“半角问题”:
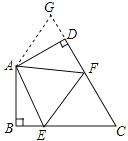
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究此“半角问题”的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;(直接写结论,不需证明)
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“∠BAD=120°,∠EAF=60°”换为∠EAF=![]() ∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
(3)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
(4)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
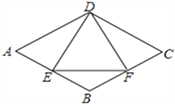
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④当AD=4时,△DEF的面积的最小值为![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com