
【题目】阅读并完成下列证明:如图,AB∥CD,∠B=55°,∠D=125°,求证:BC∥DE.
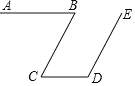
证明:AB∥CD(已知),
∴∠C=∠B( ),又∵∠B=55°( ),
∴∠C=______°(等量代换),
∵∠D=125°( ),
∴
∴BC∥DE( ).
科目:初中数学 来源: 题型:
【题目】综合题
(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.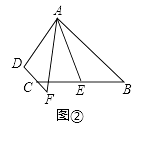
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.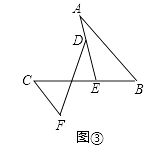
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y= ![]() (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )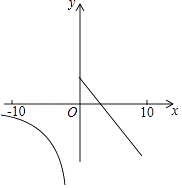
A.﹣ ![]() ≤x≤1
≤x≤1
B.﹣ ![]() ≤x≤
≤x≤ ![]()
C.﹣ ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
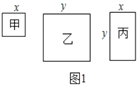
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为![]() 的正方形,乙种纸片是边长为
的正方形,乙种纸片是边长为![]() 的正方形,丙种纸片是长为
的正方形,丙种纸片是长为![]() ,宽为
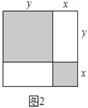
,宽为![]() 的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
(理解应用)
(1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(拓展升华)
(2)利用(1)中的等式解决下列问题.
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为 . 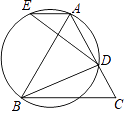
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 、
、![]() 、
、![]() 都是射线,
都是射线,![]() ,
,![]() 与
与![]() 互为余角.
互为余角.

(1)![]() 与
与![]() 有何关系?请证明你的结论;
有何关系?请证明你的结论;
(2)![]() 与
与![]() 有何关系?请证明你的结论;
有何关系?请证明你的结论;
(3)![]() 与
与![]() 有何关系?请证明你的结论.
有何关系?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com