
����Ŀ����ͼ1����֪������y=![]() x2��
x2��![]() x��3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD
x��3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD

��1�������A��B��D�����ꣻ
��2����ͼ1�����߶�OB��x�����ƶ����ҵ�O��B�ƶ���Ķ�Ӧ��ΪO����B������β˳�����ӵ�O����B����D��C�����ı���O��B��DC��������ı���O��B��DC���ܳ���Сֵ��
��3����ͼ2������M����������һ�㣬��N��y���ϣ�����CM��MN������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ��ֱ��д����N�����꣮
���𰸡���1��A����2��0����B��4��0����D��1����![]() ������2��4+
������2��4+![]() +
+![]() ����3��N��������0��
����3��N��������0��![]() ������0��
������0��![]() ������0����
������0����![]() ����0����
����0����![]() ����
����
��������
�����������1���������߽���ʽ��y=0�������x��һԪ���η��̼��������A��B�����꣬�������䷽���������߽���ʽ�����䷽���ɵó�����D�����ꣻ��2������C��0����3������x��ĶԳƵ�C����0��3��������C����0��3������ƽ��4����λ�õ���C����4��3��������DC������x���ڵ�B��������B������ƽ��4����λ�õ���O��������CO����CO�������ı���O��B��C��C��Ϊƽ���ı��Σ���ʱ�ı���O��B��DC�ܳ�ȡ��Сֵ���ٸ��������ľ��빫ʽ���CD��DC���ij��ȣ����ɵó����ۣ���3������M��λ�ò�ͬ������������ǣ�����M��ֱ��y=x��3�ϣ�����ֱ���������߽���ʽ�����M�����꣬��ϵ�C�������Լ�����ֱ�������ε����ʼ��ɵó���N�����ꣻ����M��ֱ��y=��x��3�ϣ�����ֱ���������߽���ʽ�����M�����꣬��ϵ�C�������Լ�����ֱ�������ε����ʼ��ɵó���N�����꣮�ۺ�����������ɵó����ۣ�
�����������1����y=![]() x2��
x2��![]() x��3��y=0����
x��3��y=0����![]() x2��
x2��![]() x��3=0����ã�x1=��2��x2=4����A����2��0����B��4��0������y=
x��3=0����ã�x1=��2��x2=4����A����2��0����B��4��0������y=![]() x2��
x2��![]() x��3=
x��3=![]() ��x2��2x����3=
��x2��2x����3=![]() ��x��1��2��
��x��1��2��![]() ����D��1����
����D��1����![]() ������2����y=
������2����y=![]() x2��
x2��![]() x��3��x=0����y=��3����C��0����3����D��1����
x��3��x=0����y=��3����C��0����3����D��1����![]() ����O��B��=OB=4����ͼ1��
����O��B��=OB=4����ͼ1��
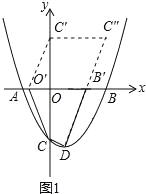
����C��0����3������x��ĶԳƵ�C����0��3��������C����0��3������ƽ��4����λ�õ���C����4��3��������DC������x���ڵ�B��������B������ƽ��4����λ�õ���O��������CO����C��O�������ı���O��B��C��C��Ϊƽ���ı��Σ���ʱ�ı���O��B��DC�ܳ�ȡ��Сֵ����ʱC�ı���O��B��DC=CD+O��B��+CO��+DB��=CD+O��B��+DC������O��B��=4��CD=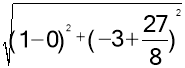 =
=![]() ��C��D=
��C��D=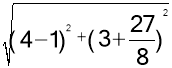 =
=![]() �����ı���O��B��DC���ܳ���СֵΪ4+
�����ı���O��B��DC���ܳ���СֵΪ4+![]() +
+![]() ����3����CMN����MNΪֱ�DZߵĵ���ֱ�������η������������ͼ2����
����3����CMN����MNΪֱ�DZߵĵ���ֱ�������η������������ͼ2����
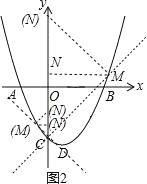 ��������C��ֱ��y=x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�
��������C��ֱ��y=x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã� ����ã�
����ã�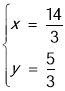 ��
��![]() ����ȥ������M��
����ȥ������M��![]() ��
��![]() �����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0��
�����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0��![]() ����0��
����0��![]() ����������C��ֱ��y=��x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�
����������C��ֱ��y=��x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�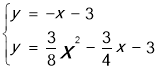 ����ã�
����ã�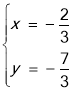 ��
��![]() ����ȥ������M����
����ȥ������M����![]() ����
����![]() �����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0����
�����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0����![]() ����0����
����0����![]() �������Ͽ�֪������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����N������Ϊ��0��
�������Ͽ�֪������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����N������Ϊ��0��![]() ������0��
������0��![]() ������0����
������0����![]() ����0����
����0����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AC��BC����ACB��90������D��E�ֱ���AC��BC�ϣ���CD��CE��

��1����ͼ1����֤����CAE����CBD��
��2����ͼ2��F��BD���е㣬��֤��AE��CF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�麬45����ֱ�����ǰ�ABC, AB=AC, ��BAC=90���� ��DΪ����CB��һ�㣬�Ҳ����C,��B�غ�,����AD.����A���߶�AD�Ĵ���l,��ֱ��l�ϣ���ȡAE=AD(��E���C��ֱ��AD��ͬ��)������CE.
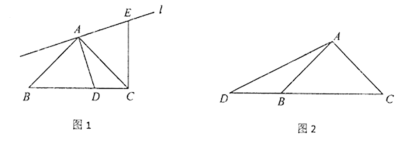
��1������D���߶�CB��ʱ����ͼ1,�߶�CE��BD��������ϵΪ____________��λ�ù�ϵΪ___________��
��2������D���߶�CB���ӳ�����ʱ����ͼ2,
���뽫ͼ�β�������;
�ڣ�1���еĽ����Ƿ��Գ���?�����������֤��;�������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ǰ���ʡ��ɫˮ��������ʡ���ز�֮һ������س������ǹ���������ݮ����ʾ�����أ�С��ӳ���ͨ��ij��ݹ�˾���ڱ��������Ѽ�һ�в�ݮ�����ʱ�����˽�����˾����ȡÿ��8Ԫ�İ�װ���⣬��ݮ������1ǧ���շ�22Ԫ������1ǧ�ˣ������ְ�ÿǧ��10Ԫ���շ��ã���ù�˾�ӳ��ᵽ������IJ�ݮ�ķ���Ϊy��Ԫ�������IJ�ݮΪx��ǧ�ˣ�
��1����y��x֮��ĺ�����ϵʽ��
��2����֪С�����欿����2.5ǧ�˲ݶ������������ο�ĵķ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��y����![]() x+m��x�ύ�ڵ�A��ֱ��l2��y��2x+n��y�ύ�ڵ�B����ֱ��l1���ڵ�P��2��2�������PAB�����Ϊ_____��
x+m��x�ύ�ڵ�A��ֱ��l2��y��2x+n��y�ύ�ڵ�B����ֱ��l1���ڵ�P��2��2�������PAB�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() �������ȣ���
�������ȣ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ����
����![]() �ij��ǣ� ��
�ij��ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס���������A�dz���������ʻ��B�ǣ���������ʻ�����У��ס��������뿪A�ǵľ���y��ǧ�ף���׳���ʻ��ʱ��t��ʱ��֮��Ĺ�ϵ��ͼ��ʾ���۲�ͼ��ش��������⣺
��1��A��B��������� ��ǧ��
��2��������ͬʱ�������ҳ����ȼ׳��絽�� ��Сʱ��
��3���ҳ��ĺ�����ϵʽΪ�� ����
��4���׳������� ����ʱ����������
��5�����ҳ���ʻ������/�������� ��Сʱ���ס����������40ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӱ�½���人�У��ɳ�����ͨ�г����������֪��������ʻ·����100ǧ�ף���ͨ�г�����ʻ·���Ǹ�������ʻ·�̵�1.3��.
��1������ͨ�г�����ʻ·�̣�
��2����Ƹ�����ƽ���ٶȣ�ǧ��/ʱ������ͨ�г�ƽ���ٶȣ�ǧ��/ʱ����2.5�����ҳ�����������ʱ��ȳ�����ͨ�г�����ʱ������45���ӣ��������ƽ���ٶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬��A=30�㣬BC=6��
��1��ʵ���������߹���ͼ����д������������ͼ�ۼ���
������ABC�Ľ�ƽ���߽�AC�ڵ�D��
�����߶�BD�Ĵ�ֱƽ���ߣ���AB�ڵ�E����BC�ڵ�F������DE��DF��
��2���������㣺�ı���BFDE�����Ϊ�� ����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com