
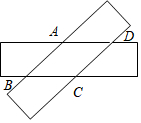
 两个长为9,宽为3的全等矩形叠合而得到四边形ABCD(不完全重合),则四边形ABCD面积的最大值为15.
两个长为9,宽为3的全等矩形叠合而得到四边形ABCD(不完全重合),则四边形ABCD面积的最大值为15. 分析 首先根据图1,证明四边形ABCD是菱形;然后判断出菱形的一条对角线为矩形的对角线时,四边形ABCD的面积最大,设AB=BC=x,则BE=9-x,利用勾股定理求出x的值,即可求出四边形ABCD面积的最大值是多少.
解答 解:如图1,作AE⊥BC于E,AF⊥CD于F,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形的宽都是3,
∴AE=AF=3,
∵S四边形ABCD=AE•BC=AF•CD,
∴BC=CD,
∴平行四边形ABCD是菱形.
如图2, ,
,
设AB=BC=x,则BE=9-x,
∵BC2=BE2+CE2,
∴x2=(9-x)2+32,
解得x=5,
∴四边形ABCD面积的最大值是:5×3=15.
故答案为15.
点评 此题主要考查了菱形的判定和性质,矩形的性质和应用,以及勾股定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:填空题
 如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°;⑤DB平分∠ADC.其中正确的结论有:①②③④(填序号)
如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°;⑤DB平分∠ADC.其中正确的结论有:①②③④(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com