
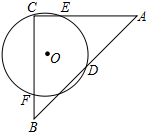
 如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )
如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |
分析 要求△CEF的面积,关键是求出CE和CF的乘积,根据题目中条件可以证明△EDC≌△FDB,得到CE和BF的关系,再根据勾股定理和⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,可以求得CE和CF的乘积,本题得以解决.
解答  解:连接CD、ED、DF、EF,如右图所示,
解:连接CD、ED、DF、EF,如右图所示,
∵AC⊥BC,AC=BC,点D是AB中点,
∴CD=DA=DB,∠CDB=90°,∠ECD=∠FBD=45°,
又∵EF是⊙O的直径,
∴∠EDF=90°,
∴∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
在△EDC和△FDB中,
$\left\{\begin{array}{l}{∠ECD=∠FBD}\\{CD=BD}\\{∠EDC=∠FDB}\end{array}\right.$,
∴△EDC≌△FDB(ASA),
∴CE=BF,
又∵AC=BC,AC=2+2$\sqrt{2}$,
∴BC=2+2$\sqrt{2}$,
即BF+FC=2+2$\sqrt{2}$,
∴CF+CE=2+2$\sqrt{2}$,
又∵∠ECF=90°,⊙O的半径为$\sqrt{3}$,
∴CE2+CF2=EF2,EF=2$\sqrt{3}$,
解得,CE•CF=4$\sqrt{2}$,
∴△CEF的面积为:$\frac{CE•CF}{2}=2\sqrt{2}$,
故选B.
点评 本题考查圆周角定理、全等三角形的判定与性质、勾股定理,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用三角形全等和勾股定理解答.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:填空题
 如图,P是线段AB上异于端点的动点,且AB=6,分别以AP、BP为边,在AB的同侧作等边△APM和等边△BPN,则△MNP外接圆半径的最小值为$\sqrt{3}$.
如图,P是线段AB上异于端点的动点,且AB=6,分别以AP、BP为边,在AB的同侧作等边△APM和等边△BPN,则△MNP外接圆半径的最小值为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这两条弦都是直径 | B. | 这两条弦最多有一条是直径 | ||
| C. | 这两条弦都不是直径 | D. | 这两条弦至少有一条是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 1 | 2 | 3 | 4 | … |
| 2 | 4 | 6 | 8 | … |
| 3 | 6 | 9 | 12 | … |
| 4 | 8 | 12 | 16 | … |
| … | … | … | … | … |
| 10 | |
| a | |
| 21 |
| A. | 16 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com