
·ÖĪö £Ø1£©ĻČÅŠ¶Ļ³ö”÷BDF”Õ”÷CDM½ų¶ųµĆ³öMC=BF£¬”ĻM=”ĻBFM£®ŌŁÅŠ¶Ļ³ö”ĻM=”ĻMACµĆ³öAC=MC¼“æÉµĆ³ö½įĀŪ£»
£Ø2£©ĻČÅŠ¶Ļ³öĖıߊĪMFGNŹĒĘ½ŠŠĖıߊĪ£¬ŌŁÅŠ¶Ļ³öMN=FG=DE=4£¬½ų¶ųÅŠ¶Ļ³öMF”ĶBCŹ±£¬ĖıߊĪMFGNµÄÖܳ¤×īŠ”£¬×īŗó¹¹Ōģ³öÖ±½ĒČż½ĒŠĪĒó³öAH¼“æÉµĆ³ö½įĀŪ£®
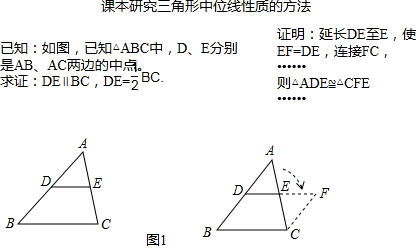
½ā“š £Ø1£©ŃÓ³¤ADÖĮµćM£¬Ź¹MD=FD£¬Į¬½ÓMC£¬
ŌŚ”÷BDFŗĶ”÷CDMÖŠ£¬$\left\{\begin{array}{l}{BD=CD}\\{”ĻBDF=”ĻCDM}\\{DF=DM}\end{array}\right.$£¬
”ą”÷BDF”Õ”÷CDM£ØSAS£©£®
”ąMC=BF£¬”ĻM=”ĻBFM£®
”ßEA=EF£¬
”ą”ĻEAF=”ĻEFA£¬
”ß”ĻAFE=”ĻBFM£¬
”ą”ĻM=”ĻMAC£¬
”ąAC=MC£¬
”ąBF=AC£»
¹Ź“š°øĪŖ£ŗŃÓ³¤ADÖĮµćM£¬Ź¹MD=FD£¬Į¬½ÓMC£¬
ŌŚ”÷BDFŗĶ”÷CDMÖŠ£¬$\left\{\begin{array}{l}{BD=CD}\\{”ĻBDF=”ĻCDM}\\{DF=DM}\end{array}\right.$£¬
”ą”÷BDF”Õ”÷CDM£ØSAS£©£®
”ąMC=BF£¬”ĻM=”ĻBFM£®
”ßEA=EF£¬
”ą”ĻEAF=”ĻEFA£¬
”ß”ĻAFE=”ĻBFM£¬
”ą”ĻM=”ĻMAC£¬
”ąAC=MC£¬
”ąBF=AC£»
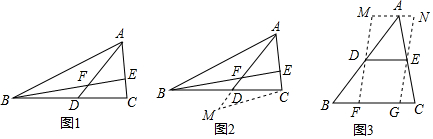
£Ø2£©ČēĶ¼£¬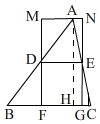
”ßMN”ĪBC£¬FM”ĪGN£¬
”ąĖıߊĪMFGNŹĒĘ½ŠŠĖıߊĪ£¬
”ąMF=NG£¬MN=FG£¬
”ßDEŹĒ”÷ABCµÄÖŠĪ»Ļߣ¬
”ąDE=$\frac{1}{2}$BC=4£¬DE”ĪBC£¬
”ąMN=FG=$\frac{1}{2}$BC=4£¬
”ąĖıߊĪMFGNÖܳ¤=2£ØMF+FG£©=2MF+8£¬
”ąMF”ĶBCŹ±£¬MF×ī¶Ģ£¬
¼“£ŗĖıߊĪMFGNµÄÖܳ¤×īŠ”£¬
¹żµćA×÷AH”ĶBCÓŚH£¬
”ąFM=AH
ŌŚRt”÷ABHÖŠ£¬”ĻB=45”ć£¬AB=10£¬
”ąAH=$\frac{10}{\sqrt{2}}$=5$\sqrt{2}$£¬
”ąĖıߊĪMFGNµÄÖܳ¤×īŠ”ĪŖ2MF+8=10$\sqrt{2}$+8£®
¹Ź“š°øĪŖ10$\sqrt{2}$+8£®
µćĘĄ “ĖĢāŹĒČż½ĒŠĪ×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖČ«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬Čż½ĒŠĪµÄÖŠĪ»Ļߣ¬Ę½ŠŠĖıߊĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬Ę½ŠŠĻß¼äµÄ¾ąĄė£¬½ā£Ø1£©¹Ų¼üŹĒ”÷BDF”Õ”÷CDM£¬½ā£Ø2£©µÄ¹Ų¼üŹĒÅŠ¶Ļ³öMF”ĶBCŹ±£¬ĖıߊĪMFGNµÄÖܳ¤×īŠ”£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
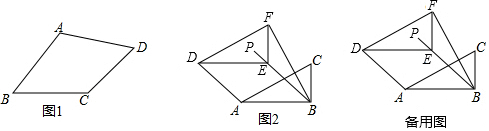
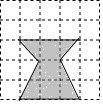 ČēĶ¼£¬·½øńĶ¼ÖŠŠ”Õż·½ŠĪµÄ±ß³¤ĪŖ1£®½«·½øńĶ¼ÖŠŅõÓ°²æ·ÖĶ¼ŠĪ¼ōĻĀĄ“£¬ŌŁ°Ń¼ōĻĀµÄŅõÓ°²æ·ÖÖŲŠĀ¼ōĘ“³ÉŅ»øöÕż·½ŠĪ£Ø²»ÖŲµžĪŽ·ģĻ¶£©£¬ÄĒĆ“ĖłĘ“³ÉµÄÕāøöÕż·½ŠĪµÄ±ß³¤ĪŖ$\sqrt{6}$£®
ČēĶ¼£¬·½øńĶ¼ÖŠŠ”Õż·½ŠĪµÄ±ß³¤ĪŖ1£®½«·½øńĶ¼ÖŠŅõÓ°²æ·ÖĶ¼ŠĪ¼ōĻĀĄ“£¬ŌŁ°Ń¼ōĻĀµÄŅõÓ°²æ·ÖÖŲŠĀ¼ōĘ“³ÉŅ»øöÕż·½ŠĪ£Ø²»ÖŲµžĪŽ·ģĻ¶£©£¬ÄĒĆ“ĖłĘ“³ÉµÄÕāøöÕż·½ŠĪµÄ±ß³¤ĪŖ$\sqrt{6}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
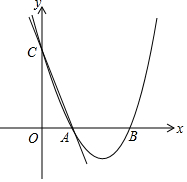 ČēĶ¼ĖłŹ¾£¬Ö±ĻßAC£ŗy=-2x+2ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻßy=ax2 +bx+c£Øa£¾0£©¹żA£¬CĮ½µć£¬ÓėxÖį½»ÓŚĮķŅ»µćB£ØBŌŚAµÄÓŅ²ą£©£¬ĒŅ”÷OBC”×”÷OCA£®
ČēĶ¼ĖłŹ¾£¬Ö±ĻßAC£ŗy=-2x+2ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻßy=ax2 +bx+c£Øa£¾0£©¹żA£¬CĮ½µć£¬ÓėxÖį½»ÓŚĮķŅ»µćB£ØBŌŚAµÄÓŅ²ą£©£¬ĒŅ”÷OBC”×”÷OCA£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1cm£¬1cm£¬1cm | B£® | 5cm£¬5cm£¬10cm | C£® | 1cm£¬2cm£¬3cm | D£® | 2cm£¬3cm£¬6cm |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
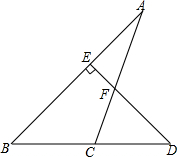 ČēĶ¼£¬DE”ĶAB£¬”ĻA=25”ć£¬”ĻD=45”ć£¬Ēó”ĻACDµÄ¶ČŹż£®
ČēĶ¼£¬DE”ĶAB£¬”ĻA=25”ć£¬”ĻD=45”ć£¬Ēó”ĻACDµÄ¶ČŹż£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com