证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BDA=∠BDP,
∴△BDA∽△PDB,
∴BD
2=AD•DP,
∵DI=DB,
∴DI
2=DP•AD;
(2)∵DI=DB,
∴∠IBD=∠BID
∵∠CBI=∠IBD-∠CBD,∠ABI=∠BID-∠BAD,
∴∠ABI=∠CBI;
(3)∵∠BAC=120°,
∴∠BAD=∠CAD=60°,
∴∠CBD=∠BCD=60°,
∴△BCD为等边三角形,
∵⊙O的半径为

,
∴BC=3,
∴S
△BDC=

.
分析:(1)根据题意可推出∠BAD=∠CBD,即可推出△BDA∽△PDB,所以BD
2=AD•DP,即DI
2=DP•AD;
(2)根据题意和外角的性质,即可推出∠IBD=∠BID,∠CBI=∠IBD-∠CBD,∠ABI=∠BID-∠BAD,即∠ABI=∠CBI;
(3)根据题意可推出△BCD为等边三角形,由⊙O的半径即可推出BC的长度和△BCD的面积.
点评:本题主要考查相似三角形的判定和性质、等边三角形的判定和性质、圆周角定理,关键在于熟练地运用个定理性质,求△BDA∽△PDB,△BCD为等边三角形.

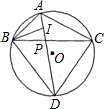 I,使DI=DB.
I,使DI=DB. ,∠BAC=120°,求△BDC的面积?
,∠BAC=120°,求△BDC的面积? ,
, .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案