
ЁОЬтФПЁПдФЖСВФСЯЃК
ЖдгкСНИіе§Ъ§aЁЂbЃЌдђ![]() ЃЈЕБЧвНіЕБaЃНbЪБШЁЕШКХЃЉЃЎ
ЃЈЕБЧвНіЕБaЃНbЪБШЁЕШКХЃЉЃЎ
ЕБ![]() ЮЊЖЈжЕЪБЃЌ
ЮЊЖЈжЕЪБЃЌ![]() газюаЁжЕЃЛЕБ
газюаЁжЕЃЛЕБ![]() ЮЊЖЈжЕЪБЃЌ
ЮЊЖЈжЕЪБЃЌ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ
Р§ШчЃКвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
НтЃКгЩ![]() Ён
Ён![]() ЃЌЕУ
ЃЌЕУ![]() Ён
Ён![]() ЃЌЕБЧвНіЕБ
ЃЌЕБЧвНіЕБ![]() МД
МД![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЮЊ
газюаЁжЕЃЌзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
ИљОнЩЯУцЕФдФЖСВФСЯЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌдђЕБ
ЃЌдђЕБ![]() ЁЁЪБЃЌ
ЁЁЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЮЊ ЁЁЃЛ
газюаЁжЕЃЌзюаЁжЕЮЊ ЁЁЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ШЁКЮжЕЪБЃЌ
ШЁКЮжЕЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃП
газюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃП
ЃЈ3ЃЉгУГЄЮЊ![]() РщАЪЮЇвЛИіГЄЗНаЮЛЈдАЃЌЮЪетИіГЄЗНаЮЛЈдАЕФГЄЁЂПэИїЮЊЖрЩйЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
РщАЪЮЇвЛИіГЄЗНаЮЛЈдАЃЌЮЪетИіГЄЗНаЮЛЈдАЕФГЄЁЂПэИїЮЊЖрЩйЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]()
![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЪЧ
газюаЁжЕЃЌзюаЁжЕЪЧ![]() ЃЛЃЈ3ЃЉЕБГЄЗНаЮЛЈдАЕФГЄЁЂПэОљЮЊ
ЃЛЃЈ3ЃЉЕБГЄЗНаЮЛЈдАЕФГЄЁЂПэОљЮЊ![]() ЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ
ЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн![]() ЛЏМђЧѓжЕМДПЩЕУЃЛ
ЛЏМђЧѓжЕМДПЩЕУЃЛ
ЃЈ2ЃЉЯШНЋyБфаЮЮЊ![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЛЏМђЧѓжЕМДПЩЕУЃЛ
ЛЏМђЧѓжЕМДПЩЕУЃЛ
ЃЈ3ЃЉЩшетИіГЄЗНаЮЛЈдАЕФГЄЮЊ![]() ЃЌдђПэЮЊ
ЃЌдђПэЮЊ![]() ЃЌдйИљОнГЄЗНаЮЕФУцЛ§ЙЋЪНПЩЕУ
ЃЌдйИљОнГЄЗНаЮЕФУцЛ§ЙЋЪНПЩЕУ![]() ЃЌШЛКѓРћгУ
ЃЌШЛКѓРћгУ![]() ЛЏМђЧѓжЕМДПЩЕУЃЎ
ЛЏМђЧѓжЕМДПЩЕУЃЎ
ЃЈ1ЃЉгЩ![]() ЕУ
ЕУ![]()
ЕБЧвНіЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЮЊ12
газюаЁжЕЃЌзюаЁжЕЮЊ12
ЙЪД№АИЮЊЃК![]() ЃЌ12ЃЛ
ЃЌ12ЃЛ
ЃЈ2ЃЉ![]()
![]()
гЩ![]() ЕУ
ЕУ![]()
ЕБЧвНіЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЮЊ9
газюаЁжЕЃЌзюаЁжЕЮЊ9
Д№ЃК![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЪЧ9ЃЛ
газюаЁжЕЃЌзюаЁжЕЪЧ9ЃЛ
ЃЈ3ЃЉЩшетИіГЄЗНаЮЛЈдАЕФГЄЮЊ![]() ЃЌдђПэЮЊ
ЃЌдђПэЮЊ![]()
дђЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§ЮЊ![]()
гЩЬтвтЕУЃК![]() ЃЌМД
ЃЌМД![]()
гЩ![]() ЕУ
ЕУ![]() ЃЌМД
ЃЌМД![]()
ЕБЧвНіЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]()
дђЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЃЌзюДѓжЕЮЊ625
газюДѓжЕЃЌзюДѓжЕЮЊ625
Д№ЃКЕБГЄЗНаЮЛЈдАЕФГЄЁЂПэОљЮЊ![]() ЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ
ЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() ЃЎ
ЃЎ


 ПкЫуЬтЬьЬьСЗЯЕСаД№АИ
ПкЫуЬтЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ10ЗжЃЉШчЭМЃЌжБЯп![]() КЭ
КЭ![]() ЯрНЛгкЕуAЃЌЧвЗжБ№гыxжсНЛгкBЃЌCСНЕуЃЌЙ§ЕуAЕФЫЋЧњЯп
ЯрНЛгкЕуAЃЌЧвЗжБ№гыxжсНЛгкBЃЌCСНЕуЃЌЙ§ЕуAЕФЫЋЧњЯп![]() ЃЈ
ЃЈ![]() ЃЉгыжБЯп
ЃЉгыжБЯп![]() ЕФСэвЛНЛЕуЮЊЕуDЃЎ
ЕФСэвЛНЛЕуЮЊЕуDЃЎ
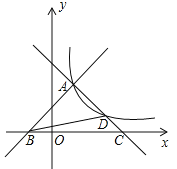
ЃЈ1ЃЉЧѓЫЋЧњЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїBCDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
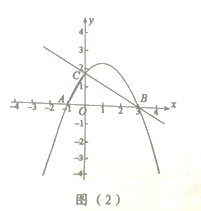
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊдЕуЃЌХзЮяЯп
ЮЊдЕуЃЌХзЮяЯп![]() ОЙ§
ОЙ§![]() Ш§ЕуЃЌЧвЦфЖдГЦжсЮЊ
Ш§ЕуЃЌЧвЦфЖдГЦжсЮЊ![]() ЦфжаЕу
ЦфжаЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЂйШчЭМЃЈ1ЃЉЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЕБЫФБпаЮ
ЩЯЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЕБЫФБпаЮ![]() ЕФУцЛ§ШЁзюДѓжЕЪБЃЌЧѓЕу
ЕФУцЛ§ШЁзюДѓжЕЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкШчЭМЃЈ2ЃЉЃЌСЌНг![]() дкХзЮяЯпЩЯгавЛЕу
дкХзЮяЯпЩЯгавЛЕу![]() Тњзу
Тњзу![]() ЃЌЧыжБНгаДГіЕу
ЃЌЧыжБНгаДГіЕу![]() ЕФКсзјБъЃЎ
ЕФКсзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГЙЋдАЩшМЦНкШеЯЪЛЈАкЗХЗНАИЃЌЦфжавЛИіЛЈЬГгЩвЛХњЛЈХшЖбГЩСљНЧЖтЃЌЖЅВувЛИіЃЌвдЯТИїВуЖбГЩСљБпаЮЃЌж№ВуУПБпдіМгвЛИіЛЈХшЃЌдђЕкЦпВуЕФЛЈХшЕФИіЪ§ЪЧЃЈ ЃЉ

A.91B.126C.127D.169
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() гы
гы![]() жсНЛгкAЃЌBСНЕуЃЌгы
жсНЛгкAЃЌBСНЕуЃЌгы![]() жсНЛгкЕуCЃЌСЌНгBCЃЎ
жсНЛгкЕуCЃЌСЌНгBCЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжБЯпBCЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуPЪЧХзЮяЯпЩЯЮЛгкЕквЛЯѓЯоФкЕФвЛЕуЃЌСЌНгPCЃЌPBЃЌЕБЁїPCBУцЛ§зюДѓЪБЃЌвЛЖЏЕуQДгЕуPДгГіЗЂЃЌбиЪЪЕБТЗОЖдЫЖЏЕН![]() жсЩЯЕФФГИіЕуGДІЃЌдйбиЪЪЕБТЗОЖдЫЖЏЕН
жсЩЯЕФФГИіЕуGДІЃЌдйбиЪЪЕБТЗОЖдЫЖЏЕН![]() жсЩЯЕФФГИіЕуHДІЃЌзюКѓЕНДяЯпЖЮBCЕФжаЕуFДІЭЃжЙЃЌЧѓЕБЁїPCBУцЛ§зюДѓЪБЃЌЕуPЕФзјБъМАЕуQдкећИідЫЖЏЙ§ГЬжаОЙ§ЕФзюЖЬТЗОЖЕФГЄЃЛ
жсЩЯЕФФГИіЕуHДІЃЌзюКѓЕНДяЯпЖЮBCЕФжаЕуFДІЭЃжЙЃЌЧѓЕБЁїPCBУцЛ§зюДѓЪБЃЌЕуPЕФзјБъМАЕуQдкећИідЫЖЏЙ§ГЬжаОЙ§ЕФзюЖЬТЗОЖЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЁїPCBУцЛ§зюДѓЪБЃЌАбХзЮяЯп![]() ЯђгвЦНвЦЪЙЫќЕФЭМЯѓОЙ§ЕуPЃЌЕУЕНаТХзЮяЯп
ЯђгвЦНвЦЪЙЫќЕФЭМЯѓОЙ§ЕуPЃЌЕУЕНаТХзЮяЯп![]() ЃЌдкаТХзЮяЯп
ЃЌдкаТХзЮяЯп![]() ЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЁїECBЕФУцЛ§ЕШгкЁїPCBЕФУцЛ§ЃЎШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЁїECBЕФУцЛ§ЕШгкЁїPCBЕФУцЛ§ЃЎШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЙ§ЕуDзїDEЁЮACЧвDE=OCЃЌСЌНгCEЁЂOEЃЌСЌНгAEНЛODгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКOE=CDЃЛ
ЃЈ2ЃЉШєСтаЮABCDЕФБпГЄЮЊ4ЃЌЁЯABC=60ЁуЃЌЧѓAEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌЧвЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+cЉmЃН0УЛгаЪЕЪ§ИљЃЌдђЯТСаНсТлЃКЂйb2Љ4acЃО0ЃЛЂкacЃМ0ЃЛЂлmЃО2ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ

A.0B.1C.2D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕНгЕНвЛХњВњЦЗЕФЩњВњШЮЮёЃЌАДвЊЧѓБиаыдк15ЬьФкЭъГЩЃЎвбжЊУПМўВњЦЗЕФЪлМлЮЊ65дЊЃЌЙЄШЫМзЕкxЬьЩњВњЕФВњЦЗЪ§СПЮЊyМўЃЌyгыxТњзуШчЯТЙиЯЕЃК
y=![]() .
.
ЃЈ1ЃЉЙЄШЫМзЕкМИЬьЩњВњЕФВњЦЗЪ§СПЮЊ80МўЃП
ЃЈ2ЃЉЩшЕкxЬьЃЈ0ЁмxЁм15ЃЉЩњВњЕФВњЦЗГЩБОЮЊPдЊ/МўЃЌPгыxЕФКЏЪ§ЭМЯѓШчЭМЃЌЙЄШЫМзЕкxЬьДДдьЕФРћШѓЮЊWдЊЃЎ
ЂйЧѓPгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЧѓWгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЕкМИЬьЪБЃЌРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
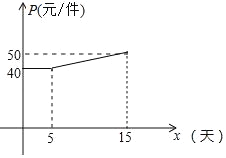
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЭјИёжНжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЪЧ1ИіЕЅЮЛГЄЖШЃЌУПИіаЁе§ЗНаЮЕФЖЅЕуНазіИёЕуЃЌЕуAЃЌBЃЌCЃЌDОљТфдкИёЕуЩЯЃЌЕуEЪЧABЕФжаЕуЃЌЙ§ЕуEзїEFЁЮADЃЌНЛBCгкЕуFЃЌзїAGЁЭEFЃЌНЛFEбгГЄЯпгкЕуGЃЌдђЯпЖЮEGЕФГЄЖШЪЧ_____ЃЎ
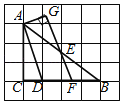
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com