
【题目】在直角△ABC中,∠ACB=90°,点E在AC边上,连结BE,作∠ACF=∠CBE交AB于点F,同时点D在BE上,且CD⊥AB.

(1)已知:如图,![]() =1,
=1,![]() .
.
①求证:△ACF≌△BCD.
②求![]() 的值.
的值.
(2)若![]() =2,
=2,![]() ,则
,则![]() 的值是多少(直接写出结果)
的值是多少(直接写出结果)
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.
(1)第5个“三角形数”是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个“正方形数”是 .
(2)除“1”以外,请再写一个既是“三角形数”,又是“正方形数”的数 .
(3)经探究我们发现:任何一个大于1的“正方形数”都可以看做两个相邻“三角形数”之和. 例如:①4=1+3;②9=3+6;③16=6+10;④ ;⑤ ;…请写出上面第4个和第5个等式.
(4)在(3)中,请探究n2= + 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的说法正确的有( )
①一个有理数不是整数就是分数;
② 0既不是整数也不是分数;
③一个有理数不是正数就是负数;
④一个分数不是正的就是负的.
A. 1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年春节期间,在网络上搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因市场竞争激烈,国商进行促销活动,决定对学习用品进行打八折出售,打折前,买2本笔记本和1支圆珠笔需要18元,买1本笔记本和2支圆珠笔需要12元.
(1)求打折前1本笔记本,1支圆珠笔各需要多少元.
(2)在促销活动时间内,购买50本笔记本和40支圆珠笔共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交![]() 轴于
轴于![]() 、B两点,交y轴于C点,其中B点的坐标为(3,0).
、B两点,交y轴于C点,其中B点的坐标为(3,0).
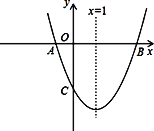
(1)直接写出![]() 点的坐标;
点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com