
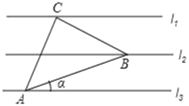
【题目】如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
过点A作AD⊥l1于D,过点B作BE⊥l1于E,根据同角的余角相等求出∠CAD=∠BCE,然后利用“角角边”证明△ACD和△CBE全等,根据全等三角形对应边相等可得CD=BE,然后利用勾股定理列式求出AC,再根据等腰直角三角形斜边等于直角边的![]() 倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,设l1,l2,l3间的距离为1,
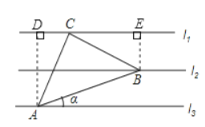
∵∠CAD+∠ACD=90°,
∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在等腰直角△ABC中,AC=BC,
在△ACD和△CBE中,∠CAD=∠BCE,∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS),
∴CD=BE=1,
在Rt△ACD中,AC=![]()
在等腰直角△ABC中,AB=![]() AC=
AC=![]() ,
,
∴sinα=![]() .
.
故选:D.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
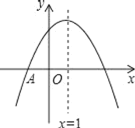
【题目】如图抛物线![]() 与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(不包含端点),则下列结论:①a+b=0;②
与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(不包含端点),则下列结论:①a+b=0;②![]() ;③若点(-2,y1),
;③若点(-2,y1),![]() ,(2,y3)在此抛物线上,则y1<y2<y3;④当1<x<3时,总有ax2+bx+c>0;⑤关于x的方程ax2+bx+c=n-1有两个不相等的实数根.正确的是( )
,(2,y3)在此抛物线上,则y1<y2<y3;④当1<x<3时,总有ax2+bx+c>0;⑤关于x的方程ax2+bx+c=n-1有两个不相等的实数根.正确的是( )
A.①②④⑤B.①②③④C.④⑤D.②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
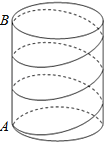
【题目】如图,圆柱底面半径为![]() cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cmB.30cmC.2![]() cmD.4
cmD.4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
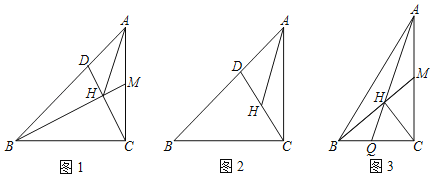
【题目】如图,在Rt△ABC中,![]() =n,M为BC上的一点,连接BM.
=n,M为BC上的一点,连接BM.
(1)如图1,若n=1,
①当M为AC的中点,当BM⊥CD于H,连接AH,求∠AHD的度数;
②如图2,当H为CD的中点,∠AHD=45°,求![]() 的值和∠CAH的度数;
的值和∠CAH的度数;
(2)如图3,CH⊥AM于H,连接CH并延长交AC于Q,M为AC中点,直接写出tan∠BHQ的值(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABDE是平行四边形,C为边B D延长线上一点,连结AC、CE,使AB=AC.
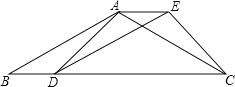
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,P,Q分别在AB,BC的延长线上,BP=CQ,连接AQ,DP交于点O,并分别与CD,BC交于点F,E,连接AE.下列结论:
①AQ⊥DP
②OA2=OEOP
③S△AOD=S四边形OECF
④当BP=1时,tan∠OAE=![]()
其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某口罩加工厂有![]() 两组工人共
两组工人共![]() 人,
人,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩![]() 只.
只.
(1)求![]() 两组工人各多少人;
两组工人各多少人;
(2)由于疫情加重![]() 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名![]() 组工人和一名
组工人和一名![]() 组工人每小时共可生产口罩
组工人每小时共可生产口罩![]() 只,若
只,若![]() 两组工人每小时至少加工
两组工人每小时至少加工![]() 只口罩,那么
只口罩,那么![]() 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com