
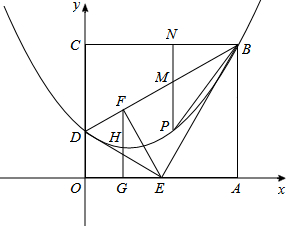
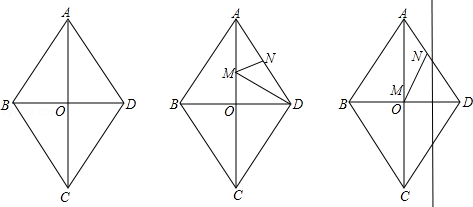
 ����B,H, D���㣬�������߽���ʽ��
����B,H, D���㣬�������߽���ʽ��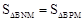 ������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
������ڣ������P�����ꣻ��������ڣ���˵�����ɣ� ����B��4
����B��4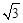 ��6����
��6����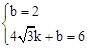 �����
�����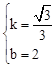 ��
��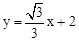 ��
��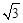 ����FE=AE=2
����FE=AE=2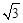 ��
��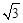 ����OG=
����OG=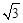 ��
��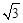 ��
��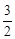 ����
����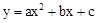 ����B��H��D���㣬
����B��H��D���㣬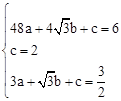 �����
�����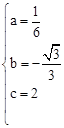 ��
�� ��
�� ����M��x��
����M��x��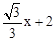 ����N��x��6����
����N��x��6���� ��
��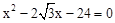 ����ã�x=2
����ã�x=2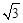 ��x=4
��x=4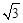 ��
��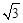 ʱ��
ʱ�� ��
��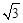 ʱ��
ʱ��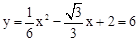 �����B�غϣ����������⣬��ȥ��
�����B�غϣ����������⣬��ȥ��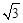 ��2����
��2����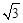 ��2����
��2����

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
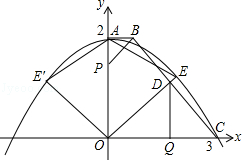
 ����A��B���㣬��A����y����࣬P�������Ϊ��0����4��������PA��PB��������˵����
����A��B���㣬��A����y����࣬P�������Ϊ��0����4��������PA��PB��������˵���� ʱ��BP2=BO•BA��
ʱ��BP2=BO•BA�� ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

 �ϣ���������߶�Ӧ�ĺ�������ʽ��
�ϣ���������߶�Ӧ�ĺ�������ʽ��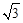 ����m��ֵ��
����m��ֵ�� �����ʱBP�ij��ȣ�
�����ʱBP�ij��ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
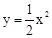 ����A��B���㣮
����A��B���㣮
 �ĺ���ֵΪy2����y1��y2����x��ȡֵ��Χ��
�ĺ���ֵΪy2����y1��y2����x��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ����������
���������� �ϣ���
�ϣ��� �Ǹ������ߵĶ��㣬��
�Ǹ������ߵĶ��㣬�� ����
���� ��ȡֵ��Χ�ǡ� ��
��ȡֵ��Χ�ǡ� ��A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
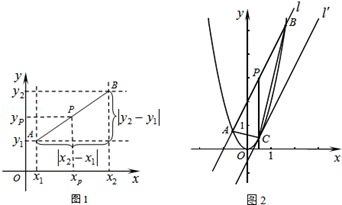
 ��ͬ��
��ͬ�� ������AB���е�����Ϊ
������AB���е�����Ϊ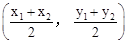 ���ɹ��ɶ�����
���ɹ��ɶ����� ������A��B�����ľ��빫ʽΪ
������A��B�����ľ��빫ʽΪ ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

| A��a��0��b��0��c��0��b2��4ac��0 | B��a��0��b��0��c��0��b2��4ac��0 |
| C��a��0��b��0��c��0��b2��4ac��0 | D��a��0��b��0��c��0��b2��4ac��0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com