【题目】如图，在大小为4×4的正方形网格中，是相似三角形的是（ ）
A. ①和② B. ②和③ C. ①和③ D. ②和④
【答案】C
【解析】分别求得四个三角形三边的长，再根据三角形三边分别成比例的两三角形相似来判定．解：∵①中的三角形的三边分别是：2，
，
；
②中的三角形的三边分别是：3，，
；
③中的三角形的三边分别是：2，2，2；
④中的三角形的三边分别是：3，
，4；
∵①与③中的三角形的三边的比为：1：
∴①与③相似．
故选C．
“点睛”此题主要考查相似三角形的判定方法：（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；（2）三边法：三组对应边的比相等的两个三角形相似；（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（4）两角法：有两组角对应相等的两个三角形相似．
夺冠金卷全能练考系列答案科目：初中数学 来源： 题型：
【题目】甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天，且甲队单独施工45天和乙队单独施工30天的工作量相同．
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，C是线段AE上一点，△ABC、△CDE都是等边三角形，AD与BC交于点M，BE与CD交于点N。
试说明：(1)AD=BE；(2)MN//AE。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，梯形ABCD中，AB//CD，且AB=2CD，E，F分别是AB，BC的中点．
EF与BD相交于点M．
（1）求证：△EDM∽△FBM；
（2）若DB=9，求BM．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个正常人的心跳平均每分70次，一天大约跳100800次，将100800用科学记数法表示为（ ）
A.0.1008×106
B.1.008×106
C.1.008×105
D.10.08×104
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD＝1.2m，CE＝0.8m，CA＝30m（点A、E、C在同一直线上）．已知小明的身高EF是1.7m，请你帮小明求出楼高AB（结果精确到0.1m）．
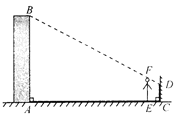
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读新知：移项且合并同类项之后，只含有偶次项的四次方程称作双二次方程．其一般形式为ax4＋bx2＋c＝0(a≠0)，一般通过换元法解之，具体解法是设 x2＝y，则原四次方程化为一元二次方程：ay2＋by＋c＝0，解出y之后代入x2＝y，从而求出x的值．
例如解：4x4－8x2＋3＝0
解：设x2＝y，则原方程可化为：4y2－8y＋3＝0
∵a＝4，b＝－8，c＝3
∴b2－4ac＝(－8)2－4×4×3＝16＞0
∴y＝
＝
∴y1＝
， y2＝
∴当y1＝时，x2＝． ∴x1＝
，x2＝－；
当y1＝时，x2＝． ∴x3＝
，x4＝－．
小试牛刀：请你解双二次方程：x4－2x2－8＝0
归纳提高：
思考以上解题方法，试判断双二次方程的根的情况，下列说法正确的是____________(选出所有的正确答案)
①当b2－4ac≥0时，原方程一定有实数根；
②当b2－4ac＜0时，原方程一定没有实数根；
③当b2－4ac≥0，并且换元之后的一元二次方程有两个正实数根时，原方程有4个实数根，换元之后的一元二次方程有一个正实数根一个负实数根时，原方程有2个实数根；
④原方程无实数根时，一定有b2－4ac＜0．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com