
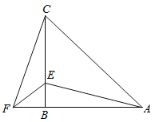
【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA=45°,F为AB延长线上一点,点E在BC上,且BE=BF.∠CAE=30°,求∠ACF的度数.
科目:初中数学 来源: 题型:
【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是 ;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
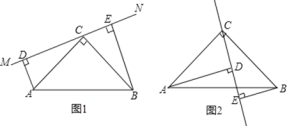
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江苏省连云港市)环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了治理大气污染,我国西部某市抽取了该市2019年中120天的空气质量指数,绘制了如下不完整的统计图表:

(1) ![]() ;
;![]() .
.
(2)请把空气质量指数的条形统计图补充完整;
(3)若绘制“空气质量指数的扇形统计图”,级别为“优”所对应扇形的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b
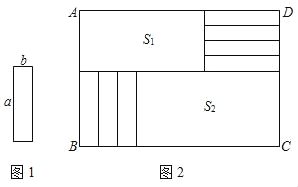
(1)当a=9,b=2,AD=30时,请求:
①长方形ABCD的面积;
②S2﹣S1的值.
(2)当AD=30时,请用含a,b的式子表示S2﹣S1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PC=PD,QC=QD,PQ,CD相交于点E.求证:PQ⊥CD.
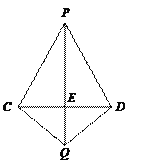
(数学思考)
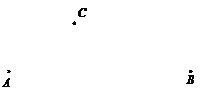
已知三个点A,B和C,只允许用圆规作点D,使得C,D两点关于AB所在的直线对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
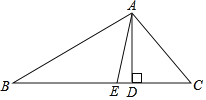
【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com