练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．计算：（$\frac{1}{2}$）100×（-2）101=-2．

    分析 根据幂的乘方和积的乘方以及同底数幂的乘法法则进行计算即可．

    解答 解：原式=：（$\frac{1}{2}$）100×（-2）100×（-2）
    =1×（-2）
    =-2，
    故答案为-2．

    点评 本题考查了幂的乘方和积的乘方，掌握运算法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

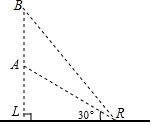    8．如图所示，运载火箭从地面L处垂直向上发射，当火箭到达A点时，从位于地面R处的雷达测得AR的距离是40km，仰角是30°．n秒后，火箭到达B点，此时仰角是45°，则火箭在这n秒中上升的高度是（20$\sqrt{3}$-20）km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

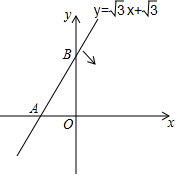    9．如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B，当直线绕着点A按顺时针方向旋转到与x轴首次重合时，点B运动的路径的长度为$\frac{2}{3}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知一元二次方程x2-3x-2=0的两个实数根为x1，x2，则（x1-1）（x2-1）的值是-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

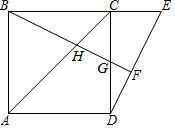    13．如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交CD于G．
    （1）求证：BG=DE；
    （2）若点G为CD的中点，求$\frac{HG}{GF}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知x为正整数，y、z与x的关系如表格所示，根据表格中的数字变化规律，解答下列问题．
    xyz
    ………
    310×3+602×10
    410×4+602×11
    510×5+602×12
    ………
    （1）分别写出y与x，z与x之间的关系式；
    （2）是否存在x的值，使得y与z相等？若存在，求出这个值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

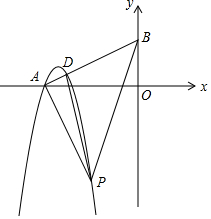    17．已知抛物线C：y=（x+2）[t（x+1）-（x+3）]，其中-7≤t≤-2，且无论t取任何符合条件的实数，点A，P都在抛物线C 上．
    （1）当t=-5 时，求抛物线C的对称轴；
    （2）当-60≤n≤-30 时，判断点（1，n）是否在抛物线C上，并说明理由；
    （3）如图，若点A在x轴上，过点A作线段AP的垂线交y轴于点B，交抛物线C于点D，当点D的纵坐标为m+$\frac{1}{2}$时，求S△PAD的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

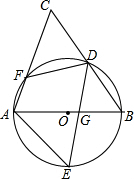    14．如图，AB是圆O的直径，D、E为圆心O上位于AB异侧的两点，连接BD并延长至点C，连接AC交圆心O于点F，连接AE、DE、DF，已知∠E=∠C．
    （1）证明：CD=BD；
    （2）若∠E=55°，求∠BDF的度数；
    （3）设DE交AB于点G，若DF=4，E是弧AB的中点，cosB=$\frac{2}{3}$，求EG•ED的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

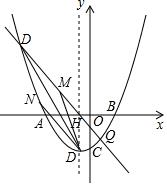    15．抛物线y=$\frac{1}{3}$x2+bx+c经过点A（-4，0）、B（2，0）两点，与y轴交于点C，顶点为D，对称轴与x轴交于点H，过点H的直线m交抛物线于P、Q两点，其中点P位于第二象限，点Q在y轴的右侧．
    （1）求D点坐标；
    （2）若∠PBA=$\frac{1}{2}$∠OBC，求点P的坐标；
    （3）设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形？若能，求出点N的坐标；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案