
科目:初中数学 来源: 题型:解答题
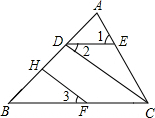 填空并完成以下证明:
填空并完成以下证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
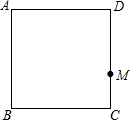 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-y=22}\\{x×2.5%+y×0.5%=n}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=22}\\{\frac{x}{2.5%}+\frac{y}{0.5%}=n}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=22}\\{x×2.5%-y×0.5%=22}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=22}\\{\frac{x}{2.5%}-\frac{y}{0.5%}=22}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
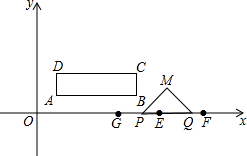 如图,矩形的四个顶点为A(1,1)、B(5,1)、C(5,2)、D(1,2),点E、F的坐标分别为(6,0)、(8,0),动点P从点E出发,以每秒2个单位长度的速度沿EO匀速运动,到达点O后立即以原来的速度沿OE返回;另一动点Q从点F出发,以每秒1个单位长度的速度沿FO匀速运动,点P、Q同时出发,两点相遇时停止运动,在点P、Q的运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQM.设运动时间为t.
如图,矩形的四个顶点为A(1,1)、B(5,1)、C(5,2)、D(1,2),点E、F的坐标分别为(6,0)、(8,0),动点P从点E出发,以每秒2个单位长度的速度沿EO匀速运动,到达点O后立即以原来的速度沿OE返回;另一动点Q从点F出发,以每秒1个单位长度的速度沿FO匀速运动,点P、Q同时出发,两点相遇时停止运动,在点P、Q的运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQM.设运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
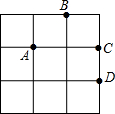 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com