Question

如图①，已知四边形ABCD是正方形，点E是AB的中点，点F在边CB的延长线上，且BE=BF，连接EF．
（1）若取AE的中点P，求证：BP=CF；
（2）在图①中，若将△BEF绕点B顺时针方向旋转α（0°＜α＜360°），如图②，是否存在某位置，使得AE∥BF？，若存在，求出所有可能的旋转角α的大小；若不存在，请说明理由；
（3）在图①中，若将△BEF绕点B顺时针旋转α（0°＜α＜90°），如图③，取AE的中点P，连接BP、CF，求证：BP=CF且BP⊥CF．

Answer 1

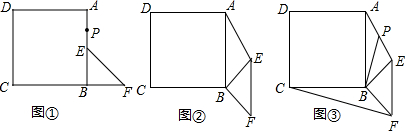
（1）证明：∵四边形ABCD是正方形，
∴BC=AB，
∵E为AB中点，P为AE中点，
∴2BE=2AE=AB，2PE=AE，
∵BE=BF，
∴CF=BC+BF=3BE，BP=BE+BE=BE，
∴BP=CF．

（2）解：存在，
∵AE∥BF，
∵EB⊥BF，
∴EB⊥AE，
∴α=∠ABE，
∵cosα==，
∴α=60°或300°．
存在，使得AE∥BF，当α=60°或300°时，AE∥BF．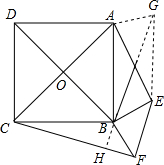

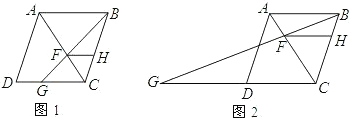
（3）证明：延长BP到G，使BP=PG，连接AG、EG，延长PB交CF于H，
∵AP=EP，BP=PG，
∴四边形ABEG是平行四边形，
∴AG=BE=BF，AG∥BE，
∴∠GAB+∠ABE=180°，
∵∠ABC=∠EBF=90°，
∴∠CBF+∠ABE=360°-180°=180°，
∴∠CBF=∠BAG，
在△AGB和△BCF中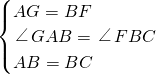
，
∴△AGB≌△BCF，
∴CF=BG=2BP，∠ABG=∠BCF，
∴∠ABG+∠CBH=180°-90°=90°，
∴∠BCF+∠CBH=90°，
∴∠CHB=180°-90°=90°，
∴BP⊥CF，BP=CF．

分析：（1）根据正方形性质得出BC=AB，根据中点定义得出2BE=2AE=AB，2PE=AE，得出BE=BF，代入求出即可；
（2）根据平行线性质得出△AEB是直角三角形，根据cotα==，求出α即可；
（3）延长BP到G，使BP=PG，连接AG、EG，延长PB交CF于H，得出四边形ABEG是平行四边形，推出AG=BE=BF，AG∥BE，求出∠CBF=∠BAG，根据SAS证△AGB≌△BCF，推出CF=BG=2BP，∠ABG=∠BCF，求出∠CHB的度数即可．
点评：本题综合考查了正方形性质，全等三角形的性质和判定，平行线的性质，三角形的内角和定理，旋转性质，垂直定义等知识点的运用，本题的综合性比较强，培养了学生综合运用性质进行推理的能力，题目较好，但是有一定的难度，对学生提出较高的要求．