
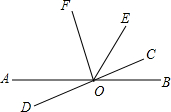
 如图.直线AB与CD相交于点O,OF⊥OC,∠BOC:∠BOE=1:3,∠AOF=2∠COE
如图.直线AB与CD相交于点O,OF⊥OC,∠BOC:∠BOE=1:3,∠AOF=2∠COE科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 气温(℃) | 11 | 13 | 14 | 15 | 16 |
| 天数(天) | 1 | 1 | 3 | 4 | 2 |
| A. | 三月下旬共有11天 | |
| B. | 三月下旬中,最低气温的众数是15℃ | |
| C. | 三月下旬中,最低气温的中位数是15℃ | |
| D. | 三月下旬中,最低气温的平均数是15℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800m,求直线l上距离D点多远的C处开挖?($\sqrt{2}$≈1.414,精确到1米)
如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800m,求直线l上距离D点多远的C处开挖?($\sqrt{2}$≈1.414,精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 70分,80分 | B. | 80分,80分 | C. | 90分,80分 | D. | 80分,90分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com