
(1)△ABC的高AD、BE相交于点H,AD的延长线交其外接圆于点G(如图).试说明为什么△BDH≌△BDG.
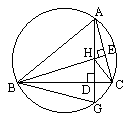
(2)在(1)的条件下,若AB=AC(如图),试判断四边形BGCH的形状,并说明理由.
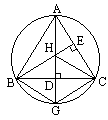
(3)如果△ABC的高AD、BE所在直线相交于圆外的点H时(如图),仍然设AB=AC,那么(2)中的结论仍然成立吗?为什么?
|
[答案](1)由已知条件知:∠CAD、∠CBE都是∠ACB的余角.∴∠CAD=∠CBE. ∵∠ CAD=∠CBG.∴∠CBE=∠CBG.∵ BD=BD,∠BDH=∠BDG=(2)四边形BGCH是菱形.理由如下: 证法 1:由(1)得△BHD≌△BDG,∴DG=DH.∴ BC垂直平分HG.∴BH=BG,CH=CG.∵ AB=AC,AD⊥BC,∴AD垂直平分BC.∴BH=CH.∴ BH=CH=CG=BG.∴四边形BGCH是菱形.证法 2:由(1)知△BDH≌△BDG.∴DH=DG.又 AB=AC,AD⊥BC,∴BD=DC.即 BC与HG互相垂直平分,∴四边形BGCH是菱形.(3)仍是菱形.理由如下: 证法 1:∵AB=AC,AD⊥BC,∴ AD垂直平分BC.∴BH=HC,BG=CG.∵∠ BHD,∠BCA都与∠HBC互余,∴∠BHD=∠BCA.又∠ BGA=∠BCA.∴∠BHD=∠BGA.∴ BH=BG.∴BH=BG=CG=HC.即 四边形 BGCH是菱形.证法 2:∵AB=AC,AD⊥BC,∴BD=DC,∠BCE=∠ABC=∠AGC.∵∠ BHD、∠BCE都与∠HBC互余,∴∠ BHD=∠BCE=∠AGC.又∠ BDH=∠CDG.∴△BDH≌△CDG.∴HD=GD.∴四边形BGCH是菱形.[剖析]本题以圆内接三角形为载体,综合考查了圆周角的性质、垂径定理、全等三角形、菱形、同角的余角等知识点.要求我们有较强的分析、探索能力及识图能力和发散思维能力. |


科目:初中数学 来源: 题型:
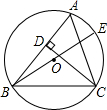 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com