
 的部分对应值如下表:
的部分对应值如下表: | … |  | 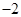 |  |  |  |  | … |
 | … |  |  |  |  |  |  | … |
 图象的对称轴为
图象的对称轴为 ,
, 对应的函数值
对应的函数值 .
. 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源:不详 题型:解答题
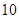 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产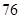 件,每件利润
件,每件利润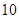 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加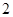 元.
元. 元时,此产品质量在第几档次?
元时,此产品质量在第几档次? 件.若生产第
件.若生产第 档的产品一天的总利润为
档的产品一天的总利润为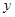 元(其中
元(其中 为正整数,且
为正整数,且 ≤
≤ ≤
≤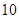 ),求出
),求出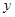 关于
关于 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线 始终有公共点,请在图一中作出这样的公共点。
始终有公共点,请在图一中作出这样的公共点。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
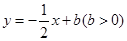 分别交
分别交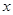 轴,
轴,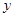 轴于
轴于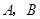 两点,以
两点,以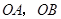 为边作矩形
为边作矩形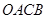 ,
,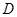 为
为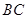 的中点.以
的中点.以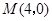 ,
,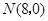 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形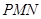 ,点
,点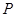 在第一象限,设矩形
在第一象限,设矩形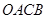 与
与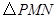 重叠部分的面积为
重叠部分的面积为 .
.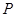 的坐标;
的坐标;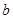 值由小到大变化时,求
值由小到大变化时,求 与
与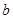 的函数关系式;
的函数关系式;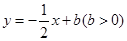 上存在点
上存在点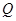 ,使
,使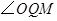 等于
等于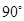 ,求出
,求出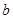 的取值范围;
的取值范围;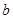 值的变化过程中,若
值的变化过程中,若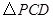 为等腰三角形,请直接写出所有符合条件的
为等腰三角形,请直接写出所有符合条件的 值.
值.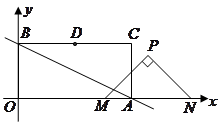
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像与
的图像与 轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.两个 | B.三个 | C.四个 | D.五个 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com