
如图,在梯形ABCD中,AD∥BC,中位线EF与对角线BD交于点G。
若EG﹕GF=2﹕3,且AD=4,则BC的长是( )

A.3 B.6 C.8 D.12
B
【解析】
试题分析:在梯形ABCD中,AD∥BC,EF为中位线,所以AD∥BC∥EF。所以在△BEG和△BAD中,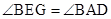 ,
, (两直线平行,同位角相等),且
(两直线平行,同位角相等),且 ,所以△BEG
,所以△BEG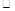 △BAD。因为EF为中位线,即点E为AB中点。所以
△BAD。因为EF为中位线,即点E为AB中点。所以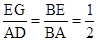 ,AD=4(已知)。所以EG=2.因为 EG﹕GF=2﹕3,可求出EF=5.根据梯形中位线的性质 梯形的中位线平行于两底,并且等于两底和的一半。求出BC=6。
,AD=4(已知)。所以EG=2.因为 EG﹕GF=2﹕3,可求出EF=5.根据梯形中位线的性质 梯形的中位线平行于两底,并且等于两底和的一半。求出BC=6。
考点:梯形中位线的性质及相似三角形性质
点评:本题难度偏低,主要考查学生对梯形中位线的性质及相似三角形性质知识点的学习。根据梯形中位线的性质 梯形的中位线平行于两底,并且等于两底和的一半,即中位线长度=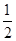 (上底+下底)。抓住重点信息具体分析所求边与已知条件之间所带的关系。如本题中求BC,要能够通过中位线公式灵活转化为求EG长度为突破口。
(上底+下底)。抓住重点信息具体分析所求边与已知条件之间所带的关系。如本题中求BC,要能够通过中位线公式灵活转化为求EG长度为突破口。


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
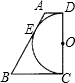 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com