
 299×(-$\frac{1}{2}$)100=$\frac{1}{2}$.
299×(-$\frac{1}{2}$)100=$\frac{1}{2}$.分析 利用积的乘方运算法则将原式变形,进而求出答案;
三角形纸片中,剪去其中一个50°的角后变成四边形,则根据多边形的内角和等于360度即可求得∠1+∠2的度数.
解答 解:299×(-$\frac{1}{2}$)100
=(-2×$\frac{1}{2}$)299×(-$\frac{1}{2}$)
=-1×(-$\frac{1}{2}$)
=$\frac{1}{2}$;
根据三角形的内角和定理得:
四边形除去∠1,∠2后的两角的度数为180°-50°=130°,
则根据四边形的内角和定理得:
∠1+∠2=360°-130°=230°.
故答案为:$\frac{1}{2}$;230°.
点评 此题主要考查了积的乘方运算,正确运用积的乘方运算法则是解题关键.同时考查了四边形的内角和是360度的实际运用与三角形内角和180度之间的关系.


科目:初中数学 来源: 题型:选择题
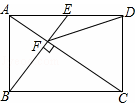 如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )| A. | AF=$\frac{1}{2}$CF | B. | ∠DCF=∠DFC | ||
| C. | 图中与△AEF相似的三角形共有4个 | D. | tan∠CAD=$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
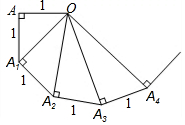 课本中有这样一句话:“利用勾股定理可以作出$\sqrt{3}$,$\sqrt{5}$,…线段(如图所示).”即:OA=1,过A作AA1⊥OA且AA1=1,根据勾股定理,得OA1=$\sqrt{2}$;再过A1作A1A2⊥OA1且A1A2=1,得OA2=$\sqrt{3}$;…以此类推,得OA2017=$\sqrt{2018}$.
课本中有这样一句话:“利用勾股定理可以作出$\sqrt{3}$,$\sqrt{5}$,…线段(如图所示).”即:OA=1,过A作AA1⊥OA且AA1=1,根据勾股定理,得OA1=$\sqrt{2}$;再过A1作A1A2⊥OA1且A1A2=1,得OA2=$\sqrt{3}$;…以此类推,得OA2017=$\sqrt{2018}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
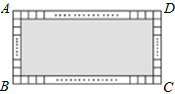 如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )
如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )| A. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)+4=52}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x:y=5:7}\\{2(x+y)+4=52}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x:y=5:7}\\{x+y=52}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)=52}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com