
����Ŀ����1����ͼ��1������֪��ABC,��AB��ACΪ������ABC�����ȱ�������ABD�͵ȱ�������ACE������BE��CD.�������ͼ�Σ���֤����BE=CD;

��2����ͼ��2������֪��ABC,��AB��ACΪ��������������ABFD��������ACGE,����BE��CD,BE��CD��ʲô������ϵ��˵�����ɣ�
��3������(1)(2)����������۵ľ����֪ʶ��������⣺��ͼ��3����Ҫ������������Ե�����B��E�ľ��룬�Ѿ���á�ABC=45�㣬��CAE=90�㣬AB=BC=1ǧ�ף�AC=AE.��BE�ij�.
���𰸡���1�������������2��BE=CD����3��![]() ǧ��
ǧ��
��������
��1�����õȱ������ε����ʣ��ñ߽DZ���֤��CAD�ա�EAB�����ɵ�BE=CD;
��2��֤��ͬ��1�����ñ߽DZ���֤��CAD�ա�EAB���ɵý����
��3���ɣ�1������2���Ľ��⾭���֪����A������ֱ��������ABD������CD�����ù��ɶ������BD��������õ���DBCΪֱ�������Σ����ù��ɶ������CD����ΪBE�ij�.
�⣺��1���ߡ�ABD����ACE���ǵȱ������Σ�
��AD=AB��AC=AE����BAD=��CAE=60��.
���BAD+��BAC=��CAE+��BAC��
�� ��CAD=��EAB.
����CAD����EAB��

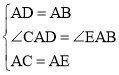 ��
��
���CAD�ա�EAB��SAS��. ��BE=CD
��2��BE=CD
����ͬ��1�������ı���ABFD��ACGE��Ϊ�����Σ�
��AD=AB��AC=AE����BAD=��CAE=90��.���CAD=��EAB.
������CAD����EAB��
AD=AB����CAD=��EAB��AC=AE
���CAD�ա�EAB��SAS������BE=CD
��3���ɣ�1������2���Ľ��⾭���֪����A������ֱ��������ABD����BAD=90��������CD��
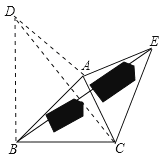
��AD=AB=1ǧ�ף���ABD=45������![]() ǧ��.
ǧ��.
����CD�����ɣ�2���ɵ�BE=CD.
�ߡ�ABC=45�������DBC=90��.
��Rt��DBC�У�BC=1ǧ�ף�![]() ǧ�ף�
ǧ�ף�
���ݹ��ɶ����ã�![]() ��ǧ�ף�.
��ǧ�ף�.
��BE=CD=![]() ǧ��.
ǧ��.


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ���9a��3b+c=0����4a��2b+c��0���۷���ax2+bx+c��4=0��������ȵ�ʵ�������ܷ���a��x��1��2+b��x��1��+c=0��������x1=��2��x2=2��������ȷ���۵ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ��O1 �͡�O2 �ཻ��A,B���㣬��O2 ������O1 ��Բ��O1,��Բ�������߽���O1�ڵ�M����AB�ڵ�N,����BM,��֪AB=2![]() .
.
��֤����1��BM�ǡ�O2�����ߣ�
��2����AM�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC����DEC��Ϊֱ�������Σ�B��C��E������һ��ֱ���ϣ���D��DM��AC��M��

��1����ͼ1������ABC�ա�DEC����AB=2BC��
����B��BN��AC��N�����߶�AN��BN��MN֮���������ϵΪ���� ������ֱ��д���𰸣�
������ME����![]() ��ֵ��
��ֵ��
��2����ͼ2����AB=CE=DE��DM=2��MC=1����ME�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��0��2����B��2��2����C��-1��-2����������F��y=x2-2mx+m2-2��ֱ��x=-2���ڵ�P��
��1����������F������Cʱ�������Ľ���ʽ��
��2�����P��������ΪyP����yP����Сֵ����ʱ������F�������㣨x1��y1������x2��y2������x1��x2��-2���Ƚ�y1��y2�Ĵ�С.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC ��,AB=CB,��ABC=90��,F Ϊ AB �ӳ�����һ��,�� E �� BC ��,�� AE=CF.

��1����֤����ABE�ա�CBF;
��2������CAE=25�����BFC ����.
��3������CAE=15�㣬BF=3.��AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ABC��,CEƽ�֡�ACB��CFƽ����ACD����EF��BC��AC��M,��CM=5,��![]() +
+![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������εĶ���Ϊ36��������������ξ��ǻƽ������Ρ���ͼ���ڡ�ABC�У�BA=BC��D �ڱ� CB �ϣ��� DB=DA=AC��

��1����ͼ1��д��ͼ�����еĻƽ������Σ���֤����
��2���� MΪ�߶� BC�ϵĵ㣬�� M��ֱ��MH��AD�� H���ֱ�ֱ�� AB��AC���N��E����ͼ 2����д���߶� BN��CE��CD֮���������ϵ��������֤��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com