
���� ��1���ȸ��ݵ�E��F������ȷ����ͼ�ε�λ�ã�Ȼ���0��a��2��a��2������������������ε���ǵ����ʵó���AOF=��EBO�������ó����ۣ�
��2���ȸ��ݵ�E��F��A��B������ȷ����BE=$\sqrt{2}$a��AF=$\sqrt{2}$b�������ã�1���ó������Ƶó�����ʽ�����ҳ�ab=2��
��3��������������������ε�����ĺͲ�ɵó����ۣ�
��� �⣺��1����AOF�ס�BEO��
���ɣ��ߵ�E��ֱ��y=-x+2�ϣ��ҵ�E�ĺ�������a��
��E��a��-a+2����
�ߵ�F��ֱ��y=-x+2�ϣ��ҵ�F����������b��
��F��2-b��b������a��0��b��0��
��-a+2��0��ʱ������0��a��2ʱ��
��ͼ1��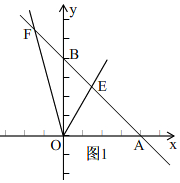 ��һ�κ���y=-x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��һ�κ���y=-x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A��2��0����B��0��2����
��OA=OB��
���OAB=��OBA=45�㣬
���BEO=��OAB+��AOE=45��+��AOE��
�ߡ�EOF=45�㣬
���AOF=��EOF+��AOE=��45��+��AOE��
���AOF=��AEO��
�ߡ�OAF=��EBO=45�㣬
���AOF�ס�BEO��
��-a+2��0ʱ������a��2ʱ��
��ͼ2��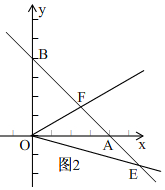 ��һ�κ���y=-x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��һ�κ���y=-x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A��2��0����B��0��2����
��OA=OB��
���OAB=��OBA=45�㣬
���BEO=��OAB-��AOE=45��-��AOE��
�ߡ�EOF=45�㣬
���AOF=��EOF-��AOE=��45��-��AOE��
���AOF=��AEO��
�ߡ�OAF=��EBO=45�㣬
���AOF�ס�BEO��
��2��ab=2��
���ɣ��ߵ�E��ֱ��y=-x+2�ϣ��ҵ�E�ĺ�������a��
��E��a��-a+2����
��B��0��2����
��BE=$\sqrt{{a}^{2}+��-a+2-2��^{2}}$=$\sqrt{2}$a
�ߵ�F��ֱ��y=-x+2�ϣ��ҵ�F����������b��
��F��2-b��b����
��A��2��0����
��AF=$\sqrt{��2-b-2��^{2}+{b}^{2}}$=$\sqrt{2}$b��
�ɣ�1��֪��OA=OB=2����AOF�ס�BEO��
��$\frac{OA}{BE}=\frac{AF}{OB}$��
��$\frac{2}{\sqrt{2}a}=\frac{\sqrt{2}b}{2}$��
��ab=2��
��3����0��a��2ʱ���ɣ�1��֪��OA=OB=2��
��S��OEF=S��AOF-S��AOE=$\frac{1}{2}$OA•|yF|-$\frac{1}{2}$OA•|yE|=$\frac{1}{2}$OA��|yF|-|yE|=$\frac{1}{2}$��2[b-��-a+2��]=a+b-2��
��a��2ʱ���ɣ�1��֪��OA=OB=2��
��S��OEF=S��AOF+S��AOE=$\frac{1}{2}$OA•|yF|+$\frac{1}{2}$OA•|yE|=$\frac{1}{2}$OA��|yF|+|yE|=$\frac{1}{2}$��2[b+��a-2��]=a+b-2��
������OEF�����Ϊa+b-2��
���� ���������������ε��ۺ��⣬��Ҫ�����������ε���ǣ����������ε��ж������ʣ������ε������ʽ�����1���Ĺؼ������������ε���ǵ����ʵó���AOF=��EBO�����2���Ĺؼ������AF=$\sqrt{2}$b��BE=$\sqrt{2}$a������ͼ���ǽⱾ����ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{25}$ | B�� | $\frac{7}{32}$ | C�� | $\frac{3}{80}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
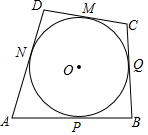 ��֪�ı���ABCD�ı�AB��BC��CD��DA�ֱ����O������P��Q��M��N��̽���ı����ı��к��ص㣮
��֪�ı���ABCD�ı�AB��BC��CD��DA�ֱ����O������P��Q��M��N��̽���ı����ı��к��ص㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 9 | C�� | $\frac{9}{2}$ | D�� | $\frac{81}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
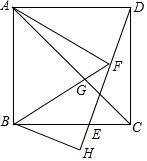 ��������ABCD�У���EΪBC���ϵ�һ�㣬����DE����FΪDE���е㣬����FA��FB���߶�FB��AC���ڵ�G����B��BH��DE��DE���ӳ����ڵ�H����BH=3��AG��GC=$\sqrt{3}$��1�����AFG�����Ϊ9$\sqrt{3}$-$\frac{27}{2}$��
��������ABCD�У���EΪBC���ϵ�һ�㣬����DE����FΪDE���е㣬����FA��FB���߶�FB��AC���ڵ�G����B��BH��DE��DE���ӳ����ڵ�H����BH=3��AG��GC=$\sqrt{3}$��1�����AFG�����Ϊ9$\sqrt{3}$-$\frac{27}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36.1��107 | B�� | 3.61��107 | C�� | 3.61��108 | D�� | 3.61��109 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 2 | C�� | 1 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com