
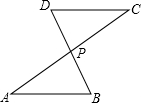
 如图,AC与BD交于点P,AP=CP,从以下四个论断①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是③.
如图,AC与BD交于点P,AP=CP,从以下四个论断①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是③. 分析 ①当添加∠B=∠D后可根据全等三角形的判定定理AAS证出△ABD≌△CDB,①可以;②当添加BP=DP后可根据全等三角形的判定定理SAS证出△ABD≌△CDB,②可以;③当添加AB=CD后,利用SSA不能证出△ABD≌△CDB,③不可以;④根据AB∥CD即可找出∠B=∠C,再根据全等三角形的判定定理ASA即可证出△ABD≌△CDB,④可以.综上即可得出结论.
解答 解:①在△ABD和△CDB中,$\left\{\begin{array}{l}{∠B=∠D}\\{∠APB=∠CPD}\\{AP=CP}\end{array}\right.$,
∴△ABD≌△CDB(AAS);
②在△ABD和△CDB中,$\left\{\begin{array}{l}{AP=CP}\\{∠APB=∠CPD}\\{BP=DP}\end{array}\right.$,
∴△ABD≌△CDB(SAS);
③∵在△ABD和△CDB中,AP=CP、∠APB=∠CPD、AB=CD不满足全等三角形的判定定理的条件,
∴添上AB=CD不能证出△APB≌△CPD;
④∵AB∥CD,
∴∠A=∠C.
在△ABD和△CDB中,$\left\{\begin{array}{l}{∠A=∠C}\\{AP=CP}\\{∠APB=∠CPD}\end{array}\right.$,
∴△ABD≌△CDB(ASA).
故答案为:③.
点评 本题考查了全等三角形的判定,熟练掌握各全等三角形的判定定理是解题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
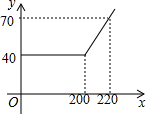 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com